题目内容
【题目】(1)操作发现
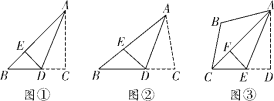
如图①,在![]() 中,
中,![]() ,点D是
,点D是![]() 上一点,沿
上一点,沿![]() 折叠
折叠![]() ,使得点C恰好落在
,使得点C恰好落在![]() 上的点E处.则
上的点E处.则![]() 的数量关系为______;
的数量关系为______;![]() ________;
________;
(2)问题解决
如图②,若(1)中![]() ,其他条件不变,请猜想
,其他条件不变,请猜想![]() 之间的关系,并证明你的结论;
之间的关系,并证明你的结论;
(3)类比探究
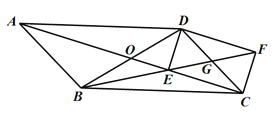
如图③,在四边形![]() 中,
中,![]() ,连接
,连接![]() ,点E是
,点E是![]() 上一点,沿
上一点,沿![]() 折叠
折叠![]() 使得点D正好落在
使得点D正好落在![]() 上的点F处,若
上的点F处,若![]() ,直接写出
,直接写出![]() 的长.
的长.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() 的长为
的长为![]() .
.
【解析】
解:(1)![]() ;
;![]()
【解法提示】如题图①,设![]() ,∵沿
,∵沿![]() 折叠
折叠![]() ,使得点C恰好落在
,使得点C恰好落在![]() 上的点E处,∴
上的点E处,∴![]() ,
,![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;![]()
(2)![]() .理由如下:
.理由如下:
如题图②,∵沿![]() 折叠
折叠![]() ,使得点C恰好落在
,使得点C恰好落在![]() 上的点E处,
上的点E处,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)![]() 的长为
的长为![]() .
.
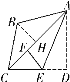
【解法提示】过点B作![]() 于点H,如图,
于点H,如图,
设![]() ,由(1)的结论得
,由(1)的结论得![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
解得![]() ,
,
即![]() 的长为
的长为![]() .
.

【题目】为了解某社区居民掌握民法知识的情况,对社区内的甲、乙两个小区各500名居民进行了测试,从中各随机抽取50名居民的成绩(百分制)进行整理、描述、分析,得到部分信息:
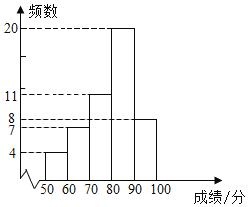
a.甲小区50名居民成绩的频数直方图如下(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
b.图中,70≤x<80组的前5名的成绩是:79 79 79 78 77
c.图中,80≤x<90组的成绩如下:
82 | 83 | 84 | 85 | 85 | 86 | 86 | 86 | 86 | 86 |
86 | 86 | 86 | 87 | 87 | 87 | 88 | 88 | 89 | 89 |
d.两组样本数据的平均数、中位数、众数、优秀率(85分及以上)、满分人数如下表所示:
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 满分人数 |
甲 | 78.58 | 84.5 | a | b | 1 |
乙 | 76.92 | 79.5 | 90 | 40% | 4 |
根据以上信息,回答下列问题:
(1)求表中a,b的值;
(2)请估计甲小区500名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,分析甲、乙两个小区参加测试的居民掌握民法知识的情况.