题目内容
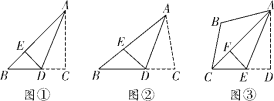
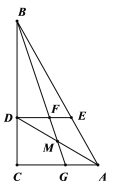
【题目】如图，在
中，∠ACB=90°，∠BAC=60°，AC=6，AD平分∠BAC，交边BC于点D，过点D作CA的平行线，交边AB于点E．
（1）求线段DE的长；
（2）取线段AD的中点M，联结BM，交线段DE于点F，延长线段BM交边AC于点G，求
的值．
【答案】（1）
；（2）
．
【解析】
（1）先根据角平分线的定义可求出
，再在
和
中，分别解直角三角形可求出
，
，从而可得
，然后利用平行线分线段成比例定理即可得；
（2）先根据线段中点的定义可得
，再根据平行线分线段成比例定理可得
，从而可得
，然后又根据平行线分线段成比例定理可得
，
，从而可得
，由此即可得出答案．
（1）
平分
，
在中，
，即
解得
在中，
，即
解得
，即
解得；
（2）如图，
点
是线段
的中点
，
，，
．
练习册系列答案
相关题目
【题目】在2019年某中学举行的冬季阳径运动会上，参加男子跳高的15名运动员的成绩如表所示：
成绩（m） | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是（ ）
A.
B.
C.
D.
