题目内容
【题目】某网店正在热销一款电子产品,其成本为10元/件,销售中发现,该商品每天的销售量y(件)与销售单价x(元/件)之间存在如图所示的关系:
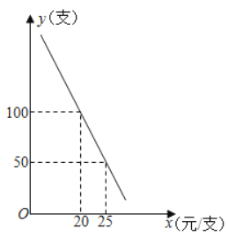
(1)请求出y与x之间的函数关系式;
(2)该款电子产品的销售单价为多少元时,每天销售利润最大?最大利润是多少元;
(3)由于武汉爆发了“新型冠状病毒”疫情,该网店店主决定从每天获得的利润中抽出300元捐赠给武汉,为了保证捐款后每天剩余利润不低于450元,如何确定该款电子产品的销售单价?
【答案】(1)y=10x+300;(2)20元时,最大利润为1000元;(3)单价每件不低于15元,且不高于25元.
【解析】
(1)利用待定系数法求解可得;
(2)设该款电子产品每天的销售利润为w元,根据“总利润=每件的利润×销售量”可得函数解析式,配方成顶点式后利用二次函数的性质求解可得;
(3)设捐款后每天剩余利润为z元,根据题意得出z=10x2+400x3000300=10x2+400x3300,求出z=450时的x的值,求解可得.
解:(1)设y与x的函数关系式为y=kx+b,
将(20,100),(25,50)代入y=kx+b,
得![]() ,
,
解得![]() ,
,
∴y与x的函数关系式为y=10x+300;
(2)设该款电子产品每天的销售利润为w元,
由题意得w=(x10)y
=(x10)(10x+300)
=10x2+400x3000
=10(x20)2+1000,
∵10<0,
∴当x=20时,w有最大值,w最大值为1000.
答:该款电子产品销售单价定为20元时,每天销售利润最大,最大销售利润为1000元;
(3)设捐款后每天剩余利润为z元,
由题意可得z=10x2+400x3000300=10x2+400x3300,
令z=450,即10x2+400x3300=450,
x240x+375=0,
解得x1=15,x2=25,
∵10<0,
∴当该款电子产品的销售单价每件不低于15元,且不高于25元时,可保证捐款后每天剩余利润不低于450元.

【题目】近几年,国内快递业务快速发展,由于其便捷、高效,人们越来越多地通过快递公司代办点来代寄包裹.某快递公司某地区一代办点对60天中每天代寄的包裹数与天数的数据(每天代寄包裹数、天数均为整数)统计如下:
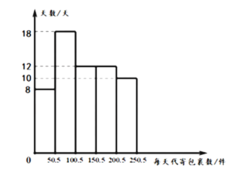
(1)求该数据中每天代寄包裹数在![]() 范围内的天数;
范围内的天数;
(2)若该代办点对顾客代寄包裹的收费标准为:重量小于或等于1千克的包裹收费8元;重量超1千克的包裹,在收费8元的基础上,每超过1千克(不足1千克的按1千克计算)需再收取2元.
①某顾客到该代办点寄重量为1.6千克的包裹,求该顾客应付多少元费用?
②这60天中,该代办点为顾客代寄的包表中有一部分重量超过2千克,且不超过5千克.现从中随机抽取40件包裹的重量数据作为样本,统计如下:
重量G(单位:千克) |
|
|
|
件数(单位:件) | 15 | 10 | 15 |
求这40件包裹收取费用的平均数.
【题目】在2019年某中学举行的冬季阳径运动会上,参加男子跳高的15名运动员的成绩如表所示:
成绩(m) | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()