题目内容
【题目】如图直角坐标系中,以M(3,0)为圆心的⊙M交x轴负半轴于A,交x轴正半轴于B,交y轴于C、D.
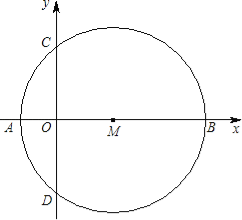
(1)若C点坐标为(0,4),求点A坐标.
(2)在(1)的条件下,在⊙M上,是否存在点P,使∠CPM=45°,若存在,求出满足条件的点P.
(3)过C作⊙M的切线CE,过A作AN⊥CE于F,交⊙M于N,当⊙M的半径大小发生变化时.AN的长度是否变化?若变化,求变化范围,若不变,证明并求值.
【答案】(1)A(﹣2,0);(2)P1(7,3),P2(﹣1,﹣3);(3)AN的长不变为6.
【解析】
(1)结合题意,连接CM,根据点M和点C的坐标可得出⊙M的半径,即MA的长,利用M的坐标即可得出A的坐标;
(2)假设存在这样的点P,根据题意,可知△CMP为等腰直角三角形,且CM=MP=5.根据圆的方程和两点直接的距离公式列出方程组,解之即可得出点P的坐标;
(3)作MH⊥AN于H,则AH=NH,易证△AMH≌△MCO,故AH=M0.从而可证AH为一定值.
(1)如图①,连接CM,
在Rt△COM中,OC=4,OM=3,CM=![]() =5,
=5,
∴AM=5,
∴OA=2,
∴A(-2,0);

(2)假设存在这样的点P(x,y),结合题意,
可得△CMP为等腰直角三角形,且CM=PM=5,
故CP=5![]() ;
;
结合题意有,
 ;
;
解之得:
![]() ,
,![]()
即存在两个这样的点P;
P1(7,3),P2(﹣1,﹣3);
(3)AN的长不变为6.
如图②,连接CM,作MH⊥AN于H,
则AH=HN,
∵EC切⊙M,
∴∠ECM=90°,
∴四边形DMCF是矩形,
∴∠CMH=90°,
在△AMH和△MCO中,
∵∠CMO=∠MAH=90°-∠AMH,
∠COM=∠ADM=90°,
CM=AM,
∴△AMH≌△MCO,
∴AH=MO=3,
即AN=HN+AH=3+3=6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】近几年,国内快递业务快速发展,由于其便捷、高效,人们越来越多地通过快递公司代办点来代寄包裹.某快递公司某地区一代办点对60天中每天代寄的包裹数与天数的数据(每天代寄包裹数、天数均为整数)统计如下:
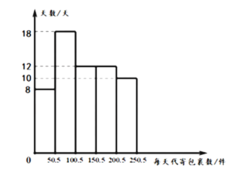
(1)求该数据中每天代寄包裹数在![]() 范围内的天数;
范围内的天数;
(2)若该代办点对顾客代寄包裹的收费标准为:重量小于或等于1千克的包裹收费8元;重量超1千克的包裹,在收费8元的基础上,每超过1千克(不足1千克的按1千克计算)需再收取2元.
①某顾客到该代办点寄重量为1.6千克的包裹,求该顾客应付多少元费用?
②这60天中,该代办点为顾客代寄的包表中有一部分重量超过2千克,且不超过5千克.现从中随机抽取40件包裹的重量数据作为样本,统计如下:
重量G(单位:千克) |
|
|
|
件数(单位:件) | 15 | 10 | 15 |
求这40件包裹收取费用的平均数.