题目内容
【题目】为了解某社区居民掌握民法知识的情况,对社区内的甲、乙两个小区各500名居民进行了测试,从中各随机抽取50名居民的成绩(百分制)进行整理、描述、分析,得到部分信息:
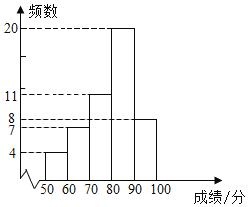
a.甲小区50名居民成绩的频数直方图如下(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
b.图中,70≤x<80组的前5名的成绩是:79 79 79 78 77
c.图中,80≤x<90组的成绩如下:
82 | 83 | 84 | 85 | 85 | 86 | 86 | 86 | 86 | 86 |
86 | 86 | 86 | 87 | 87 | 87 | 88 | 88 | 89 | 89 |
d.两组样本数据的平均数、中位数、众数、优秀率(85分及以上)、满分人数如下表所示:
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 满分人数 |
甲 | 78.58 | 84.5 | a | b | 1 |
乙 | 76.92 | 79.5 | 90 | 40% | 4 |
根据以上信息,回答下列问题:
(1)求表中a,b的值;
(2)请估计甲小区500名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,分析甲、乙两个小区参加测试的居民掌握民法知识的情况.
【答案】(1)86;50% (2)310人 (3)见解析
【解析】
(1)由众数的定义和优秀率的计算公式可求解;
(2)A小区500名居民成绩能超过平均数的人数:500×![]() =310(人);
=310(人);
(3)根据统计量:平均数、中位数、众数、优秀率,即可分析甲、乙两小区参加测试的居民掌握民法知识的情况.
解:(1)∵86出现的次数最多,
∴众数a=86,
优秀率b=![]() ×100%=50%;
×100%=50%;
(2)500×![]() =310(人),
=310(人),
答:甲小区500名居民成绩能超过平均数的人数为310人;
(3)从平均数看,甲小区居民掌握民法知识平均分比乙小区居民掌握民法知识的平均分高;
从中位数看,甲小区居民掌握民法知识的情况比乙小区居民掌握民法知识的情况好;
从众数看,乙小区居民掌握民法知识的情况比甲小区居民掌握民法知识的情况好;
从优秀率看,甲小区居民掌握民法知识的成绩优秀率比乙小区居民掌握民法知识的成绩优秀率高.

【题目】近几年,国内快递业务快速发展,由于其便捷、高效,人们越来越多地通过快递公司代办点来代寄包裹.某快递公司某地区一代办点对60天中每天代寄的包裹数与天数的数据(每天代寄包裹数、天数均为整数)统计如下:
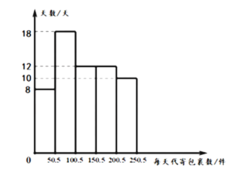
(1)求该数据中每天代寄包裹数在![]() 范围内的天数;
范围内的天数;
(2)若该代办点对顾客代寄包裹的收费标准为:重量小于或等于1千克的包裹收费8元;重量超1千克的包裹,在收费8元的基础上,每超过1千克(不足1千克的按1千克计算)需再收取2元.
①某顾客到该代办点寄重量为1.6千克的包裹,求该顾客应付多少元费用?
②这60天中,该代办点为顾客代寄的包表中有一部分重量超过2千克,且不超过5千克.现从中随机抽取40件包裹的重量数据作为样本,统计如下:
重量G(单位:千克) |
|
|
|
件数(单位:件) | 15 | 10 | 15 |
求这40件包裹收取费用的平均数.