题目内容
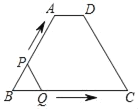
【题目】如图,在四边形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=2,BC=8,点P从点B出发沿折线BA﹣AD﹣DC匀速运动,同时,点Q从点B出发沿折线BC﹣CD匀速运动,点P与点Q的速度相同,当二者相遇时,运动停止,设点P运动的路程为x,△BPQ的面积为y,则y关于x的函数图象大致是( )
A.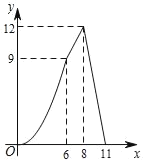 B.
B.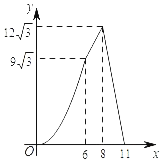
C.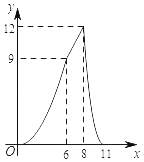 D.
D.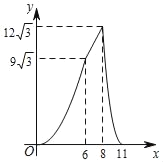
【答案】B
【解析】
①当点P在AB上运动时(0≤x≤6),![]() ,当x=6时,
,当x=6时,![]() ; ②6<x<8,
; ②6<x<8,![]() ;③当x≥8时,点PC=6+2+6-x=14-x,QC= 8-x,则PQ=22-2t,△BPQ的高常数,即可求解.
;③当x≥8时,点PC=6+2+6-x=14-x,QC= 8-x,则PQ=22-2t,△BPQ的高常数,即可求解.
解:由题意得:四边形ABCD为等腰梯形,如下图,分别过点A、D作梯形的高AM、DN交BC于点M、N,
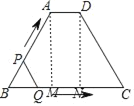
则MN=AD=2,BM=NC=![]() (BC﹣AD)=3,
(BC﹣AD)=3,
则AB=2BM=6,
①当点P在AB上运动时(0≤x≤6),
![]() ,
,
当x=6时,y=9![]() ,
,
图象中符合条件的有B、D;
②6<x<8,高为常数,
∵MN=AD=2,BM=![]() (BC- MN)=3,
(BC- MN)=3,
∴AM=BMtanB=3×![]() =3
=3![]() ,
,
则![]() ;
;
③当x≥8时,点PC=6+2+6﹣x=14﹣x,QC=x﹣8,
则PQ=22﹣2x,
而△BPQ的高常数,故y的表达式为一次函数,
故在B、D中符合条件的为B,
故选:B.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目