题目内容
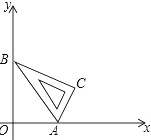
【题目】如图,将含有30°角的直角三角板ABC放入平面直角坐标系,顶点A,B分别落在x、y轴的正半轴上,∠OAB=60°,点A的坐标为(1,0),将三角板ABC沿x轴向右作无滑动的滚动(先绕点A按顺时针方向旋转60°,再绕点C按顺时针方向旋转90°,…)当点B第一次落在x轴上时,则点B运动的路径与坐标轴围成的图形面积是________.
【答案】![]() +
+![]() π
π
【解析】在Rt△AOB中,由A点坐标得OA=1,根据锐角三角形函数可得AB=2,OB=![]() ,在旋转过程中,三角板的角度和边的长度不变,所以点B运动的路径与坐标轴围成的图形面积:S=
,在旋转过程中,三角板的角度和边的长度不变,所以点B运动的路径与坐标轴围成的图形面积:S=![]() ,计算即可得出答案.
,计算即可得出答案.
在Rt△AOB中,∵A(1,0),∴OA=1,
又∵∠OAB=60°,
∴cos60°=![]() ,
,
∴AB=2,OB=![]() ,
,
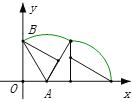
∵在旋转过程中,三角板的角度和边的长度不变,
∴点B运动的路径与坐标轴围成的图形面积:
S=![]() =
=![]() π,
π,
故答案为:![]() π.
π.

练习册系列答案
相关题目