题目内容
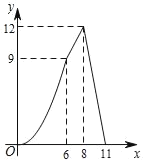
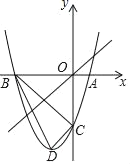
【题目】如图,已知一次函数y=kx+b的图象与反比例函数![]() 的图象相交于A(2n+1,1),B(﹣1,n﹣4)两点,与y轴相交于点C
的图象相交于A(2n+1,1),B(﹣1,n﹣4)两点,与y轴相交于点C
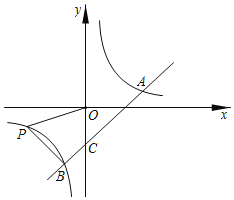
(1)反比例函数的解析式为_____,一次函数的解析式为_____;
(2)请直接写出不等式kx+b≥![]() 的解集;
的解集;
(3)过点B作BP⊥AB,交反比例函数![]() (x<0)的图象于点P,连接OP,求四边形OPBC的面积.
(x<0)的图象于点P,连接OP,求四边形OPBC的面积.
【答案】(1)![]() ,y=x﹣2;(2)﹣1≤x<0或x≥3;(3)S四边形OPBC=5.
,y=x﹣2;(2)﹣1≤x<0或x≥3;(3)S四边形OPBC=5.
【解析】
(1)把A(2n+1,1),B(﹣1,n﹣4)两点代入y=![]() ,即可求得n、m,从而得到A、B的坐标以及反比例函数的解析式,然后根据待定系数法即可求得一次函数的解析式;(2)根据函数的图象及A、B两点坐标即可求得;(3)延长BP交x轴于E,设直线AB与x轴的交点为D,求出直线BP的解析式,通过解方程组求出直线PB与双曲线的交点P的坐标,根据S四边形OPBC=S△BDE﹣S△OPE﹣S△COD即可计算.
,即可求得n、m,从而得到A、B的坐标以及反比例函数的解析式,然后根据待定系数法即可求得一次函数的解析式;(2)根据函数的图象及A、B两点坐标即可求得;(3)延长BP交x轴于E,设直线AB与x轴的交点为D,求出直线BP的解析式,通过解方程组求出直线PB与双曲线的交点P的坐标,根据S四边形OPBC=S△BDE﹣S△OPE﹣S△COD即可计算.
(1)∵反比例函数y=![]() 的图象过A(2n+1,1),B(﹣1,n﹣4)两点,
的图象过A(2n+1,1),B(﹣1,n﹣4)两点,
∴m=(2n+1)×1=﹣1×(n﹣4),
解得,m=3,n=1,
∵A(3,1),B(﹣1,﹣3),
反比例函数的解析式为y=![]() ;
;
将A(3,1),B(﹣1,﹣3)代入y=kx+b得![]() ,
,
解得![]() ,
,
∴一次函数的解析式为y=x﹣2,
故答案为y=![]() ,y=x﹣2;
,y=x﹣2;
(2)由图象可知:不等式kx+b≥![]() 的解集为﹣1≤x<0或x≥3;
的解集为﹣1≤x<0或x≥3;
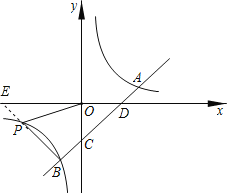
(3)延长BP交x轴于E,设直线AB与x轴的交点为D,
设直线PB为y=﹣x+b′,B(﹣1,﹣3)代入得b′=﹣4,
∴直线PB为y=﹣x-4,
∴E(﹣4,0),
由直线AB可知D(2,0),C(0,﹣2),
∴DE=6,
解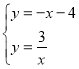 得
得![]() 或
或![]() ,
,
∴P(﹣3,﹣1),
∴S四边形OPBC=S△BDE﹣S△OPE﹣S△COD=![]() ×6×3﹣
×6×3﹣![]() ×4×1﹣
×4×1﹣![]() ×2×2=5.
×2×2=5.

 阅读快车系列答案
阅读快车系列答案