题目内容
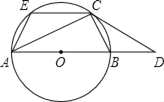
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,过C点的切线与AB的延长线交于点D,CE∥AB交⊙O于点E,连接AC、BC、AE.
(1)求证:①∠DCB=∠CAB;②CDCE=CBCA;
(2)作CG⊥AB于点G.若tan∠CAB=![]() (k>1),求
(k>1),求![]() 的值(用含k的式子表示).
的值(用含k的式子表示).
【答案】(1)见解析;(2)![]()
【解析】分析:(1)①过点C作直径CF,连接BF.即可得![]() 又由直径所对的圆周角等于直角,可得
又由直径所对的圆周角等于直角,可得![]() 又由切线的性质,可得
又由切线的性质,可得![]() 是直角,即可证得
是直角,即可证得![]() ②由EC∥AB,易证得∠4=∠3=∠BCD.有圆的内接四边形的对角互补,可得∠CBD=∠AEC.即可证得
②由EC∥AB,易证得∠4=∠3=∠BCD.有圆的内接四边形的对角互补,可得∠CBD=∠AEC.即可证得![]() 则得到
则得到![]()
(2)在![]() 与
与![]() 中,利用三角函数的性质,即可求得
中,利用三角函数的性质,即可求得![]() 的值.
的值.
详解:(1)证明:①如图1,
作直径CF,连接BF.
∴![]()
则![]()
∵CD切![]() 于C,
于C,
∴OC⊥CD,
则![]()
∴∠BCD=∠CAB.

②∵EC∥AB,∠BCD=∠3,
∴∠4=∠3=∠BCD.
∵![]()
∵![]()
∴∠CBD=∠AEC.
∴△ACE∽△DCB.
∴![]()
∴CDCE=CBCA.
(2)如图2,连接EB,交OC于点H,

∵CG⊥AB于点G,![]()
∴∠3=∠BCG.
∴AE=BC,
∠3=∠4.
∴∠3=∠EBG.
∴∠BCG=∠EBG.
∵![]()
∴在Rt△HGB中,![]()
在Rt△BCG中,![]()
设HG=a,则![]()
∵EC∥AB,
∴△ECH∽△BGH.
∴![]()

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目