题目内容
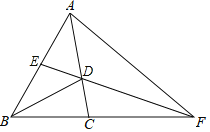
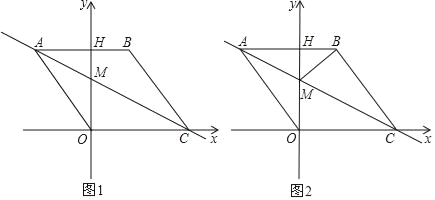
【题目】如图,四边形ABCD是平行四边形,A, B是直线l上的两点,点B关于AD的对称点为M,连接![]() 交AD于F点.
交AD于F点.
(1)若![]() ,如图,
,如图,
①依题意补全图形;
②判断MF与FC的数量关系是 ;

(2)如图,当![]() 时,
时,![]() ,CD的延长线相交于点E,取
,CD的延长线相交于点E,取![]() E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.
E的中点H,连结HF. 用等式表示线段CE与AF的数量关系,并证明.

【答案】(1)①见解析② FM=FC(2)CE=![]() AF
AF
【解析】
(1)①按要求画图即可;②根据“AAS”证明△AFM≌△DFC,即可证明结论成立;
(2)过点M作![]() ∥CD交AD于点G.先证明MG=AM,从而MG=CD,根据“AAS”可证△MFG≌ △CFD,进而GF=FD,HF是△CME的中位线,可得
∥CD交AD于点G.先证明MG=AM,从而MG=CD,根据“AAS”可证△MFG≌ △CFD,进而GF=FD,HF是△CME的中位线,可得![]() .再证明∠FHA=90°,根据勾股定理得出
.再证明∠FHA=90°,根据勾股定理得出![]() ,进而可求出线段CE与AF的数量关系.
,进而可求出线段CE与AF的数量关系.
(1)①如图,
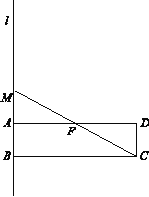
② FM=FC.
∵点B关于AD的对称点为M,
∴AB=AM.
∵四边形ABCD是平行四边形,
∴AB=CD,
∴AM=CD.
∵![]() ,
,
∴四边形ABCD是矩形,
∴∠MAF=∠CDF,
又∵∠AFM=∠CFD,
∴△AFM≌△DFC,
∴FM=FC;
(2)CE与AF的数量关系是CE=![]() AF
AF
证明:过点M作![]() ∥CD交AD于点G.
∥CD交AD于点G.
∵B,M关于AD对称,
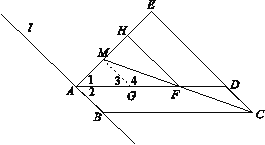
∴∠1=∠2,AB=AM.
∵四边形ABCD为平行四边形
∴AB∥CD.
∵MG∥CD,
∴MG∥AB.
∴∠2=∠3.
∴∠1=∠3.
∴AM=MG.
∵AB=AM,AB=CD,
∴MG=CD.
∵MG∥CD,
∴ ∠4=∠FDC.
∵∠MFG=∠CFD,
∴ △MFG≌ △CFD.
∴ FM=FC.
∴F为CM的中点,
∵H为ME的中点,
∴ FH∥CE,
![]()
∵∠ABC=135°, 平行四边形ABCD中,AD∥BC,
∴∠2=180°-∠ABC=45°.
∴由对称性,∠1=∠2=45°.
∵FH∥CD,AB∥CD,
∴FH∥AB.
∴∠HFA=∠2=45°.
∴∠FHA=90°,HA=HF.
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() .
.

【题目】2019年6月11日至17日是我国第29个全国节能宣传周,主题为“节能减耗,保卫蓝天”。某学校为配合宣传活动,抽查了某班级10天的用电量,数据如下表(单位:度):
度数 | 8 | 9 | 10 | 13 | 14 | 15 |
天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)这10天用电量的众数是___________,中位数是_________;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级,试估计该校6月份(30天)总的用电量.