题目内容
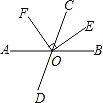
【题目】如图，直线 AB与CD相交于O，OE是∠COB的平分线，OE⊥OF．∠AOD＝74°
（1）求∠BOE的度数；
（2）试说明OF平分∠AOC．
【答案】（1）37°；（2）见解析.
【解析】
（1）根据对顶角相可得∠BOC＝∠AOD＝74°，再根据角平分线的性质解答即可；
（2）根据邻补角的性质得∠AOC＝106°，再计算出∠COF和∠AOF的度数即可．
解：（1）∵直线 AB与CD相交于O，
∴∠BOC＝∠AOD＝74°，
∵OE是∠COB的平分线，
∴∠BOE＝∠COE＝
∠BOC＝37°；
（2）∵∠AOC+∠AOD＝180°，
∴∠AOC＝180°﹣∠AOD＝180°﹣74°＝106°，
∵OE⊥OF，
∴∠EOF＝90°，
∴∠COF＝90°﹣∠COE＝90°﹣37°＝53°．
又∵∠AOF＝∠AOC﹣∠COF＝106°﹣53°＝53°，
∴∠COF＝∠AOF，
∴OF平分∠AOC．
练习册系列答案
相关题目
【题目】2019年6月11日至17日是我国第29个全国节能宣传周，主题为“节能减耗，保卫蓝天”。某学校为配合宣传活动，抽查了某班级10天的用电量，数据如下表（单位：度）：
度数 | 8 | 9 | 10 | 13 | 14 | 15 |
天数 | 1 | 1 | 2 | 3 | 1 | 2 |
（1）这10天用电量的众数是___________，中位数是_________；
（2）求这个班级平均每天的用电量；
（3）已知该校共有20个班级，试估计该校6月份（30天）总的用电量.
