题目内容
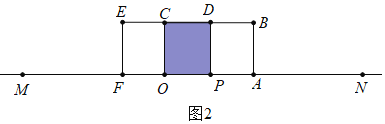
【题目】已知M、N直线l上两点,MN=20,O、P为线段MN上两动点,过O、P分别作长方形OABC与长方形PDEF(如图),其中,两边OA、PF分别在直线l上,图形在直线l的同侧,且OA=PF=4,CO=DP=3,动点O从点M出发,以1单位/秒的速度向右运动;同时,动点P从点N出发,以2单位/秒的速度向左运动,设运动的时间为t秒.
(1)若t=2.5秒,求点A与点F的距离;
(2)求当t为何值时,两长方形重叠部分为正方形;
(3)运动过程中,在两长方形没有重叠部分前,若能使线段AB、BC、AF的长构成三角形,求t的取值范围.

【答案】(1)4.5;(2)当t分别为5秒、![]() 秒时,两长方形重叠部分为正方形;(3)t的取值范围为
秒时,两长方形重叠部分为正方形;(3)t的取值范围为![]()
【解析】
(1)求出MA,NF的值即可判断;
(2)分两种情形:ABEF是正方形;OCDP是正方形.分别求解即可解决问题;
(3)求出相遇前AF=7或1时的时间即可解决问题.
解:(1)当t=2.5秒时,MA=MO+OA=2.5+4=6.5,
NF=NP+PF=2.5×2+4=9,
∴AF=20﹣6.5﹣9=4.5.
(2)第一次重叠部分为正方形ABEF(如图)此时FA=3,
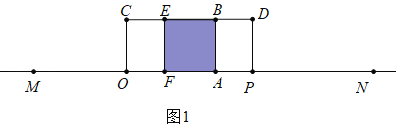
MA=t+4,NF=2t+4,
∴(t+4)+(2t+4)﹣20=3,
∴t=5.
第二次重叠部分为正方形PDCO(如图)此时OP=3,
OM=t,PN=2t,
∴20﹣t﹣2t=3,
∴t=![]() ,
,
∴当t分别为5秒、![]() 秒时,两长方形重叠部分为正方形;
秒时,两长方形重叠部分为正方形;
(3)∵线段AB、BC、AF的长构成三角形,AB=3,BC=4,
∴1<AF<7,
重叠前AF=7,则有20﹣(t+4)﹣(2t+4)=7,
解得t=![]() ;
;
AF=1,则有20﹣(t+4)﹣(2t+4)=1,
解得t=![]() ,
,
∴t的取值范围为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某天,一蔬菜经营户用90元钱按批发价从蔬菜批发市场买了西红柿和豆角共50kg,然后在市场上按零售价出售,西红柿和豆角当天的批发价和零售价如下表所示:
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 2.0 | 1.5 |
零售价(单位:元/kg) | 2.9 | 2.6 |
如果西红柿和豆角全部以零售价售出,他当天卖这些西红柿和豆角赚了多少元钱?