题目内容
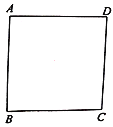
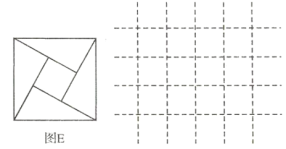
【题目】图
为2002年世界数学家大会的会标，它是用四个形状相同、大小相等的直角三角形拼成的正方形，请通过图形的运动，在右侧网格中补全此会标.
（1）问此正方形会标是旋转对称图形吗？答：______.
（2）若会标中直角三角形的两条直角边长分别为
和
，请用含
（其中
）的代数式表示出此正方形会标的面积.
【答案】图见解析，（1）是（2）
【解析】
通过平移，将图E在右侧网格中补全.
（1）根据旋转对称图形定义可知，此正方形会标是以对角线交点为中心的旋转对称图形；
（2）根据勾股定理可计算出正方形的边长，然后利用正方形面积公式即可得.
通过平移，将图E在右侧网格中补全如下：
.
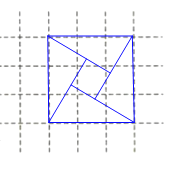（1）由已知条件可知，此正方形会标绕正方形对角线交点旋转
后，所得到的图形与原图形完全重合，故此正方形会标是旋转对称图形，
答案填“是”；
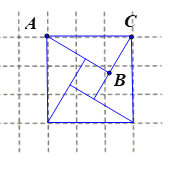
（2）由题意知，在
中，AB=4n，BC=3n，
由勾股定理得，
，
故此正方形会标的面积
，
即此正方形会标的面积为.
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
