题目内容
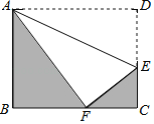
【题目】如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知AD=10cm,BF=6cm.
(1)求DE的值;
(2)求图中阴影部分的面积.
【答案】(1)5;(2)30.
【解析】
(1)由矩形的性质得BC=AD=10,CF=BC﹣BF=4,由折叠的性质得AF=AD=10,在Rt△ABF中,由勾股定理得AB=![]() =8,设EC=x,则DE=EF=8﹣x,在Rt△ECF中,由勾股定理得x2+42=(8﹣x)2,解得x=3,即可得出结果;
=8,设EC=x,则DE=EF=8﹣x,在Rt△ECF中,由勾股定理得x2+42=(8﹣x)2,解得x=3,即可得出结果;
(2)由S阴影=S△ABF+S△CEF,即可得出结果.
解:(1)∵四边形ABCD是矩形,
∴BC=AD=10,CF=BC﹣BF=10﹣6=4,
由折叠的性质得AF=AD=10,
在Rt△ABF中,由勾股定理得:AB=8,
设EC=x,则DE=EF=8﹣x,
在Rt△ECF中,由勾股定理得:x2+42=(8﹣x)2,
解得:x=3,
∴EC=3,DE=8﹣3=5(cm);
(2)S阴影=S△ABF+S△CEF=![]() ×6×8+
×6×8+![]() ×4×3=30(cm2).
×4×3=30(cm2).

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】甲、乙两名学生进行射击练习,两人在相同条件下各射击10次,将射击结果作统计分析如下:
命中环数 | 5 | 6 | 7 | 8 | 9 | 10 |
甲命中环数的次数 | 1 | 4 | 2 | 1 | 1 | 1 |
乙命中环数的次数 | 1 | 2 | 4 | 2 | 1 | 0 |
平均数 | 众数 | 方差 | |
甲 | 7 | 6 | 2.2 |
乙 |
(1)请你计算乙学生的相关数据并填入表中;
(2)根据你所学的统计学知识,利用上述某些数据评价甲、乙两人的射击水平。
【题目】某公司10名销售员,去年完成的销售额情况如表:
销售额(单位:万元) | 3 | 4 | 5 | 6 | 7 | 8 | 10 |
销售员人数(单位:人) | 1 | 3 | 2 | 1 | 1 | 1 | 1 |
(1)求销售额的平均数、众数、中位数;
(2)今年公司为了调动员工积极性,提高年销售额,准备采取超额有奖的措施,请根据(1)的结果,通过比较,合理确定今年每个销售员统一的销售额标准是多少万元?