题目内容
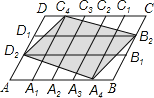
【题目】如图，在平行四边形ABCD中，点A1, A2, A3, A4和C1, C2, C3, C4分别是AB和CD的五等分点，点B1, B2和D1,D2分别是BC和DA的三等分点.已知四边形A4B2C4D2的面积为18，则平行四边形ABCD的面积为（ ）
A. 22B. 25C. 30D. 15
【答案】C
【解析】
可以设平行四边形ABCD的面积是S，根据等分点的定义利用平行四边形ABCD的面积减去四个角上的三角形的面积，就可表示出四边形A4B2C4D2的面积，从而得到两个四边形面积的关系，即可求解．
解：设平行四边形ABCD的面积是S，设AB=5a，BC=3b．AB边上的高是3x，BC边上的高是5y．
则S=5a3x=3b5y．即ax=by=
．
△AA4D2与△B2CC4全等，B2C=
BC=b，B2C边上的高是
5y=4y．
则△AA4D2与△B2CC4的面积是2by=
S．
同理△D2C4D与△A4BB2的面积是．
则四边形A4B2C4D2的面积是S-S-S--=
S，
即S=18，
解得S=30．
则平行四边形ABCD的面积为30．
故选：C．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】有20筐白菜，以每筐25千克为标准，超过或不足的分别用正、负数来表示．记录如下(单位：千克)：
与标准质量的差 | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
（1）这些白菜中，最重的一筐比最轻的一筐重多少千克？
（2）与标准重量比较，20筐白菜总计为超过或不足多少千克？
（3）)若白菜每千克售价2.6元，则这20筐白菜可卖多少元？
