题目内容
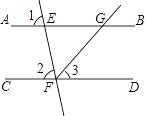
【题目】如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.
解:因为∠1=∠2=80°(已知),
所以AB∥CD__________
所以∠BGF+∠3=180°__________
因为∠2+∠EFD=180°(邻补角的性质).
所以∠EFD=________.(等式性质).
因为FG平分∠EFD(已知).
所以∠3=________∠EFD(角平分线的性质).
所以∠3=________.(等式性质).
所以∠BGF=________.(等式性质).
【答案】 同位角相等,两直线平行 两直线平行,同旁内角互补 100° ![]() 50° 130°
50° 130°
【解析】试题分析: 因为∠1和∠2是同位角,所以可以利用同位角相等判定两直线平行, 因为∠BGF和∠3是同旁内角,所以根据平行线的性质可得∠BGF+∠3=180°,然后根据角平分线的性质和等式的性质可求得所求角的度数.
试题解析:因为∠1=∠2=80°(已知), 所以AB∥CD(同位角相等,两直线平行),
所以∠BGF+∠3=180°(两直线平行,同旁内角互补),
因为∠2+∠EFD=180°(邻补角的性质),
所以∠EFD=100°(等式性质),
因为FG平分∠EFD(已知),
所以∠3= ![]() ∠EFD(角平分线的性质),
∠EFD(角平分线的性质),
所以∠3=50°(等式性质),
所以∠BGF=130°(等式性质),
故答案为:同位角相等,两直线平行;两直线平行,同旁内角互补;100°; ![]() ;50°;130°.
;50°;130°.
点睛:根据两直线平行的判定及性质求角的过程,一步步把求解的过程补充完整即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目