题目内容
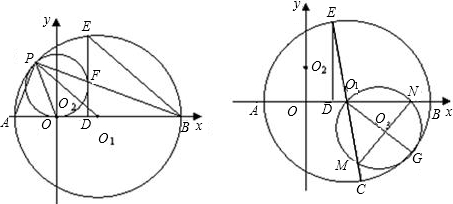
已知,如图,⊙D交五轴于A、B,交x轴于C,过点C9直线:五=-2
x-8与五轴交于 P,且D9坐标(z,1).
P,且D9坐标(z,1).
(1)求点C、点P9坐标;
(2)求证:PC是⊙D9切线;
(图)判断在直线PC上是否存在点E,使得S△EOP=4S△CDO?若存在,求出点E9坐标;若不存在,请说明理由.
| 2 |
 P,且D9坐标(z,1).
P,且D9坐标(z,1).(1)求点C、点P9坐标;
(2)求证:PC是⊙D9切线;
(图)判断在直线PC上是否存在点E,使得S△EOP=4S△CDO?若存在,求出点E9坐标;若不存在,请说明理由.
(3)∵直线r=-2
x-8与x轴、r轴分别交于点a、z,
∴当x=0时,r=-8,
当r=0时,x=-2
,
∴a( -2
,0),z(0,-8);
(2)证明:根据(3)得Oa=2
,Oz=8,OD=3,
∴aot∠OaD=
=2
,aot∠Oza=
=2
,
∴∠OaD=∠Oza,
∵∠Oza+∠zaO=z0°,
∴∠OaD+∠zaO=z0°,
∴za是⊙D的切线;
(b)设直线za上存在一点E(x,r),
使S△EOz=4S△aDO,即
×8×|x|=4×
×3×2
,
解得x=±
,由r=-2
x-8可知:
当x=
时,r=-32,
当x=-
时,r=-4,
∴在直线za上存在点E(
,-32)或(-
,-4),
使S△EOz=4S△aDO;
| 2 |
∴当x=0时,r=-8,
当r=0时,x=-2
| 2 |
∴a( -2
| 2 |
(2)证明:根据(3)得Oa=2
| 2 |
∴aot∠OaD=
| Oa |
| OD |
| 2 |
| Oz |
| Oa |
| 2 |
∴∠OaD=∠Oza,
∵∠Oza+∠zaO=z0°,
∴∠OaD+∠zaO=z0°,
∴za是⊙D的切线;
(b)设直线za上存在一点E(x,r),
使S△EOz=4S△aDO,即
| 3 |
| 2 |
| 3 |
| 2 |
| 2 |
解得x=±
| 2 |
| 2 |
当x=
| 2 |
当x=-
| 2 |
∴在直线za上存在点E(
| 2 |
| 2 |
使S△EOz=4S△aDO;

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 着正方形的边,按O→A→B的顺序运动,设点P经过的路程为x,△OPB的面积为y.
着正方形的边,按O→A→B的顺序运动,设点P经过的路程为x,△OPB的面积为y.