题目内容
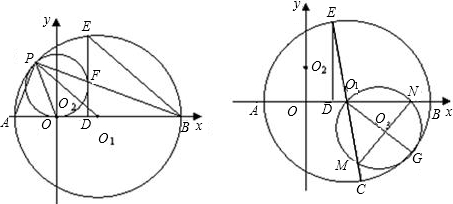
已知:如图,直线y=-
x+3交x轴于O1,交y轴于O2,⊙O2与x轴相切于O点,交直线O1O2于P点,以O1为圆心,O1P为半径的圆交x轴于A、B两点,PB交⊙O2于点F,⊙O1的弦BE=BO,EF的延长线交AB于D,连接PA、PO.
(1)求证:∠APO=∠BPO;
(2)求证:EF是⊙O2的切线;
(3)EO1的延长线交⊙O1于C点,若G为BC上一动点,以O1G为直径作⊙O3交O1C于点M,交O1B于N.下列结论:①O1M•O1N为定值;②线段MN的长度不变.只有一个是正确的,请你判断出正确的结论,并证明正确的结论,以及求出它的值.
| 3 |
| 4 |
(1)求证:∠APO=∠BPO;
(2)求证:EF是⊙O2的切线;
(3)EO1的延长线交⊙O1于C点,若G为BC上一动点,以O1G为直径作⊙O3交O1C于点M,交O1B于N.下列结论:①O1M•O1N为定值;②线段MN的长度不变.只有一个是正确的,请你判断出正确的结论,并证明正确的结论,以及求出它的值.

(1)连接O2F.
∵O2P=O2F,O1P=O1B,
∴∠O2PF=∠O2FP,∠O1PB=∠O1BP,
∴∠O2FP=∠O1BP.
∴O2F∥O1B,
得∠OO2F=90°,
∴∠OPB=
∠OO2F=45°.
又∵AB为直径,
∴∠APB=90°,
∴∠APO=∠BPO=45°.
(2)延长ED交⊙O1于点H,连接PE.
∵BO为切线,
∴BO2=BF•BP.
又∵BE=BO,
∴BE2=BF•BP.
而∠PBE=∠EBF,
∴△PBE∽△EBF,
∴∠BEF=∠BPE,
∴BE=BH,有AB⊥ED.
又由(1)知O2F∥O1B,
∴O2F⊥DE,
∴EF为⊙O2的切线.
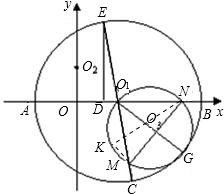
(3)MN的长度不变.
过N作⊙O3的直径NK,连接MK.则∠K=∠MO1N=∠EO1D,
且∠NMK=∠EDO1=90°,
又∵NK=O1E,
∴△NKM≌△EDO1,
∴MN=ED.
而OO1=4,OO2=3,
∴O1O2=5,
∴O1A=8.即AB=16,
∵EF与圆O2相切,
∴O2F⊥ED,
则四边形OO2FD为矩形,
∴O2F=OD,又圆O2的半径O2F=3,
∴OD=3,
∴AD=7,BD=9.
ED2=AD•BD,
∴ED=3
.
故MN的长度不会发生变化,其长度为3
.

∵O2P=O2F,O1P=O1B,
∴∠O2PF=∠O2FP,∠O1PB=∠O1BP,
∴∠O2FP=∠O1BP.
∴O2F∥O1B,
得∠OO2F=90°,
∴∠OPB=
| 1 |
| 2 |
又∵AB为直径,
∴∠APB=90°,
∴∠APO=∠BPO=45°.
(2)延长ED交⊙O1于点H,连接PE.
∵BO为切线,
∴BO2=BF•BP.
又∵BE=BO,
∴BE2=BF•BP.
而∠PBE=∠EBF,
∴△PBE∽△EBF,
∴∠BEF=∠BPE,
∴BE=BH,有AB⊥ED.
又由(1)知O2F∥O1B,
∴O2F⊥DE,
∴EF为⊙O2的切线.

(3)MN的长度不变.
过N作⊙O3的直径NK,连接MK.则∠K=∠MO1N=∠EO1D,
且∠NMK=∠EDO1=90°,
又∵NK=O1E,
∴△NKM≌△EDO1,
∴MN=ED.
而OO1=4,OO2=3,
∴O1O2=5,
∴O1A=8.即AB=16,
∵EF与圆O2相切,
∴O2F⊥ED,
则四边形OO2FD为矩形,
∴O2F=OD,又圆O2的半径O2F=3,
∴OD=3,
∴AD=7,BD=9.
ED2=AD•BD,
∴ED=3
| 7 |
故MN的长度不会发生变化,其长度为3
| 7 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 90°,∠A=60°,点A的坐标为(
90°,∠A=60°,点A的坐标为( ,0),以CD为一边在x轴上方作矩形CDEF,且CF:CD=1:2.设矩形CDEF与△ABO重叠部分的面积为S.
,0),以CD为一边在x轴上方作矩形CDEF,且CF:CD=1:2.设矩形CDEF与△ABO重叠部分的面积为S.
 P,且D9坐标(z,1).
P,且D9坐标(z,1).