题目内容
在购买某场篮球赛门票时,设购买门票张数为x(张),总费用为y(元).
方案一:若单位赞助广告费10000元,则该单位所购门票价格为每张60元.(总费用=赞助广告费+总门票费)
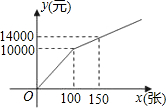
方案二:购买门票的方式如图所示.
解答下列问题:
(1)请分别求出方案二中当0≤x≤100时和当x>100时,y与x的函数关系式;
(2)若购买本场篮球赛门票是300张,你将选择哪一种方案?请说明理由;
(3)若甲、乙两个单位分别采用方案一、方案二购买本场篮球赛门票共700张,花去总费用共58000元,求甲、乙两个单位各购买门票多少张?
方案一:若单位赞助广告费10000元,则该单位所购门票价格为每张60元.(总费用=赞助广告费+总门票费)
方案二:购买门票的方式如图所示.
解答下列问题:
(1)请分别求出方案二中当0≤x≤100时和当x>100时,y与x的函数关系式;
(2)若购买本场篮球赛门票是300张,你将选择哪一种方案?请说明理由;
(3)若甲、乙两个单位分别采用方案一、方案二购买本场篮球赛门票共700张,花去总费用共58000元,求甲、乙两个单位各购买门票多少张?

(1)设当0≤x≤100时y与x的函数关系式为y1=k1x,当x>100时y与x的函数关系式y2=k2x+b,由图象得:
10000=100k1,
,
解得:k1=100,
,
故y1=100x,y2=80x+2000;
(2)设方案1的付费总费用为W元,则购买300张票时付费为:W=10000+60×300=28000元,
方案2的付费为:y2=80×300+2000=26000元,
∵28000>26000,
∴选择方案2.
(3)设采用方案1购买了x张,则用方案2购买了(700-x)张,由题意得:
10000+60x+80(700-x)+2000=58000,
解得:x=500,
故方案2买了700-500=200张.
或10000+60x+100(700-x)=58000.(700-x≤100),
解得:x=550
∴700-550=150>100(舍去)
答:甲、乙两个单位用方案1购买门票500张,用方案2购买门票200张.
10000=100k1,
|
解得:k1=100,
|
故y1=100x,y2=80x+2000;
(2)设方案1的付费总费用为W元,则购买300张票时付费为:W=10000+60×300=28000元,
方案2的付费为:y2=80×300+2000=26000元,
∵28000>26000,
∴选择方案2.
(3)设采用方案1购买了x张,则用方案2购买了(700-x)张,由题意得:
10000+60x+80(700-x)+2000=58000,
解得:x=500,
故方案2买了700-500=200张.
或10000+60x+100(700-x)=58000.(700-x≤100),
解得:x=550
∴700-550=150>100(舍去)
答:甲、乙两个单位用方案1购买门票500张,用方案2购买门票200张.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 标为(3,2),B点坐标为(1,0).
标为(3,2),B点坐标为(1,0).

 P,且D9坐标(z,1).
P,且D9坐标(z,1).