��Ŀ����
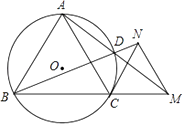
����Ŀ����ͼ��������ABCD��һ�ű߳�Ϊ12���ֵ�Ƥ�Ƥ��ʦ�����ڴ�Ƥ�������ڵĽ���ֱ����¡�PDQ���PCR��õ�һ�������PQABR������PD=2DQ��PC=RC����P��Q��
R����ֱ���CD��AD��BC�ϣ���ͼ��ʾ��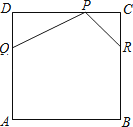
��1����Ƥ��ʦ�����¡�PDQʱ����DQ����Ϊx���֣�������x��ʾ��ʱ��PDQ�������
��2���У�1������x��ֵΪ����ʱ�������PQABR��������������˵��������ɲ�����𰸣�
���𰸡�
��1��
�⣺��DQ=x���֣�
��PD=2DQ=2x���֣�
��S��PDQ= ![]() x��2x=x2��ƽ�����֣�
x��2x=x2��ƽ�����֣�
��2��
�⣺��PD=2x���֣�CD=12���֣�
��PC=CR=12��2x�����֣���
��S�����PQABR=S������ABCD��S��PDQ��S��PCR
=122��x2�� ![]() ��12��2x��2
��12��2x��2
=144��x2�� ![]() ��144��48x+4x2��
��144��48x+4x2��
=144��x2��72+24x��2x2
=��3x2+24x+72=
��3��x2��8x+42��+72+3��16
=��3��x��4��2+120��
�ʵ�x=4ʱ�������PQABR��������Ϊ120ƽ�����֣�
����������1������������ʾ��PD���Ӷ��õ���PDQ�������
����������2���ֱ����������ABCD���������PDQ����PCR��������������������ε���������ȷ����ȡ��ֵʱ��xֵ���������ı����ۺ��⣬��Ҫ����������������ļ��㣬���������ļ��㷽�����Ȿ��Ĺؼ��������ε�����ļ��㣮
�����㾫�������������ε��������Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪�����ε����=1/2���ס��ߣ�

����Ŀ��ij���ڳ��д�����У���Ҫ��ֲ![]() ��
��![]() ���ֲ�ͬ�����繲
���ֲ�ͬ�����繲![]() �ã����б꣬�а�����
�ã����б꣬�а�����![]() ��Ԫ�ı����б�а�������̣����ݵ��鼰������ϱ�����
��Ԫ�ı����б�а�������̣����ݵ��鼰������ϱ����� ![]() ��
��![]() ��������ijɱ��ۼ��ɻ��������
��������ijɱ��ۼ��ɻ��������
Ʒ�� | ����ۣ�Ԫ/�ã� | �ɻ��� |
|
|
|
|
|
|
����ֲ![]() ������
������![]() �ã��а��̻�õ�����Ϊ
�ã��а��̻�õ�����Ϊ![]() Ԫ��
Ԫ��
��![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��![]() ������Ҫ����ֲ��������ijɻ��ʲ�����
������Ҫ����ֲ��������ijɻ��ʲ�����![]() ���а���Ӧ���ѡ��������ܻ�����������������Ƕ��٣�
���а���Ӧ���ѡ��������ܻ�����������������Ƕ��٣�