题目内容
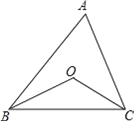
【题目】如图,⊙O是等边△ABC的外接圆,M是BC延长线上一点,连接AM交⊙O于点D,延长BD至点N,使得BN=AM,连接CN,MN. 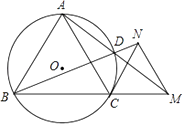
(1)判断△CMN的形状,并证明你的结论;
(2)求证:CN是⊙O的切线;
(3)若等边△ABC的边长是2,求ADAM的值.
【答案】
(1)解:△CMN为等边三角形.理由如下:
∵△ABC为等边三角形,
∴CB=CA,∠ABC=∠ACB=60°,
在△BCN和△ACM中
 ,
,
∴△BCN≌△ACM,
∴CN=CM,∠BCN=∠ACM,
∴∠ACB+∠ACN=∠ACN+∠MCN,
∴∠MCN=∠ACB=60°,
∴△CMN为等边三角形
(2)证明:连接OC,如图,
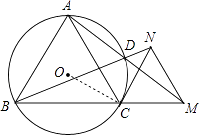
∵CA=CB,
∴ ![]() =
= ![]() ,
,
∴OC⊥AB,
∵∠ABC=∠MCN=60°,
∴AB∥CN,
∴OC⊥CN,
∴CN是⊙O的切线
(3)解:连接CD,如图,
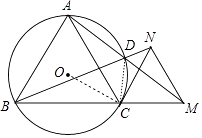
∵∠ADC+∠ABC=180°,∠ACM+∠ACB=180°,
而∠ABC=∠ACB=60°,
∴∠ADC=∠ACM,
而∠DAC=∠CAM,
∴△ACD∽△AMC,
∴AC:AD=AM:AC,
∴ADAM=AC2,
∵等边△ABC的边长是2,
∴AC=2,
∴ADDM=4.
【解析】(1)利用等边三角形的性质得到CB=CA,∠ABC=∠ACB=60°,再证明△BCN≌△ACM得到CN=CM,∠BCN=∠ACM,则∠MCN=∠ACB=60°,于是可判断△CMN为等边三角形;(2)连接OC,如图,利用CA=CB得到 ![]() =
= ![]() ,则根据垂径定理的推论得到OC⊥AB,再证明AB∥CN,则OC⊥CN,然后根据切线的判定方法可判断CN是⊙O的切线;(3)连接CD,如图,证明△ACD∽△AMC,利用相似比得到ADAM=AC2 , 然后利用等边△ABC的边长是2可得到ADDM的值.
,则根据垂径定理的推论得到OC⊥AB,再证明AB∥CN,则OC⊥CN,然后根据切线的判定方法可判断CN是⊙O的切线;(3)连接CD,如图,证明△ACD∽△AMC,利用相似比得到ADAM=AC2 , 然后利用等边△ABC的边长是2可得到ADDM的值.