题目内容
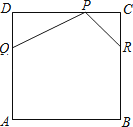
【题目】在直角三角形中,两条直角边的长度分别为a和b,斜边长度为c,则a2+b2=c2,即两条直角边的平方和等于斜边的平方,此结论称为勾股定理.在一张纸上画两个同样大小的直角三角形ABC和A′B′C′,并把它们拼成如图所示的形状 (点C和A′重合,且两直角三角形的斜边互相垂直).请利用拼得的图形证明勾股定理.

【答案】见解析
【解析】
连接![]() ,梯形的面积等于上底加下底的和乘以高除以2,,用字母表示出来,化简后,即可得证.
,梯形的面积等于上底加下底的和乘以高除以2,,用字母表示出来,化简后,即可得证.
如图所示,

在Rt△ABC中,
∵∠1+∠2=90°,∠1=∠3,∴∠2+∠3=90°.
又∵∠ACC′=90°,
∴∠2+∠3+∠ACC′=180°,
∴B,C(A′),B′在同一条直线上.
又∵∠B=90°,∠B′=90°,
∴∠B+∠B′=180°,∴AB∥C′B′.
由面积相等得![]() (a+b)(a+b)=
(a+b)(a+b)=![]() ab+
ab+![]() ab+
ab+![]() c2,
c2,
即a2+b2=c2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备选体育用品 | 篮球 | 排球 | 羽毛球拍 |
单价(元) | 50 | 40 | 25 |
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?(若能实现直接写出一种答案即可,若不能请说明理由.)