题目内容
【题目】坐标平面上,某二次函数图形的顶点为(2,﹣1),此函数图形与x轴相交于P、Q两点,且PQ=6.若此函数图形通过(1,a)、(3,b)、(﹣1,c)、(﹣3,d)四点,则a、b、c、d之值何者为正?( )
A.a
B.b
C.c
D.d
【答案】D
【解析】解:∵二次函数图形的顶点为(2,﹣1),
∴对称轴为x=2,
∵ ![]() ×PQ=
×PQ= ![]() ×6=3,
×6=3,
∴图形与x轴的交点为(2﹣3,0)=(﹣1,0),和(2+3,0)=(5,0),
已知图形通过(2,﹣1)、(﹣1,0)、(5,0)三点,
如图,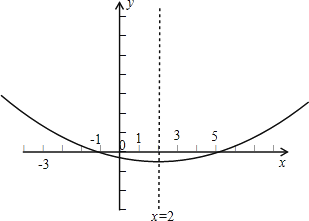
由图形可知:a=b<0,c=0,d>0.
故选:D.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目