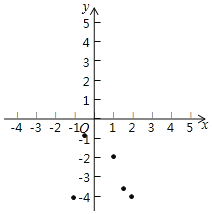题目内容
【题目】在△ABC中,∠ABC=90°
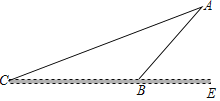
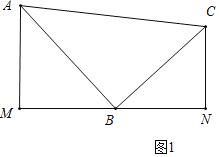
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为点M,N,求证:△ABM∽△BCN;
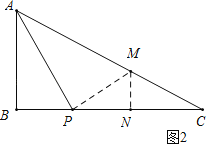
(2)如图2,P是BC边上一点,∠BAP=∠C,tan∠PAC=![]() ,BP=2cm,求CP的长.
,BP=2cm,求CP的长.

【答案】(1)详见解析;(2)8.
【解析】
(1)利用相似三角形的判定易证△ABM∽△BCN;
(2)过P作PM⊥AP,交AC于M,过M作MN⊥PC于N,先证△PMN∽△ABP,求出PN与AB的比,设PN=2t,则AB=![]() t,推出CN=PN=2t,再证△ABP∽△CBA,利用相似三角形对应边的比相等即可求出t的值,进一步求出CP的值.
t,推出CN=PN=2t,再证△ABP∽△CBA,利用相似三角形对应边的比相等即可求出t的值,进一步求出CP的值.
(1)证明:∵AM⊥MN,CN⊥MN,
∴∠M=∠N=90°
∴∠MAB+∠ABM=90°,
∵∠ABC=90°,
∴∠ABM+∠CBN=90°,
∴∠MAB=∠CBN,
∴△ABM∽△BCN;
(2)解:如图2,过P作PM⊥AP,交AC于M,过M作MN⊥PC于N,
则∠APB+∠MPN=90°,∠APB+∠BAP=90°,
∴∠MPN=∠BAP,
又∵∠B=∠N=90°,
∴△PMN∽△ABP,
∴![]() ,
,
设PN=2t,则AB=![]() t,
t,
∵∠BAP=∠MPN,∠BAP=∠C,
∴∠MPC=∠C,
∴CN=PN=2t,
∵∠B=∠B=90°,∠BAP=∠C,
∴△ABP∽△CBA,
∴![]() ,
,
∴(![]() t)2=2×(2+4t),
t)2=2×(2+4t),
解得,x1=2,x2=![]() (舍去),
(舍去),
∴PC=CN+PN=4t=4×2=8.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案【题目】小浩根据学习函数的经验,对函数![]() 的图像和性质进行深入探究,过程如下,请补充完整.
的图像和性质进行深入探究,过程如下,请补充完整.
自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应数值如下表:
的几组对应数值如下表:
| … |
|
|
|
|
| 0 | 0.5 | 1 | 1.5 | 2 |
| … |
| … |
|
|
|
|
| 0 |
|
|
|
| 0 | … |
表中![]() 的值是_______.
的值是_______.
(2)如图,在平面直角坐标系![]() 中,描出了以上表中部分对应值为坐标的点,根据描出的点,画出该函数的图像.
中,描出了以上表中部分对应值为坐标的点,根据描出的点,画出该函数的图像.
(3)类比抛物线![]() ,试从图像的轴对称性、增减性、有无最值三个方面分别说明函数
,试从图像的轴对称性、增减性、有无最值三个方面分别说明函数![]() 具有的性质:(各写一条即可)
具有的性质:(各写一条即可)
___________________________________________________________________________
(4)进一步探究函数图像发现:
①函数图像与![]() 轴有_______个交点,所以对应的方程
轴有_______个交点,所以对应的方程![]() 有______个实数根;
有______个实数根;
②方程![]() 有_______个实数根;
有_______个实数根;
③对关于![]() 的方程
的方程![]() ,模仿②写出一个真命题.
,模仿②写出一个真命题.
____________________________________________________________