题目内容
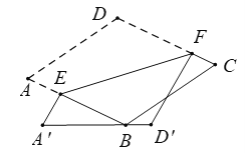
【题目】如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在点![]() ,
,![]() 处,且
处,且![]() 经过点B,EF为折痕,当
经过点B,EF为折痕,当![]() ⊥CD时,
⊥CD时,![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
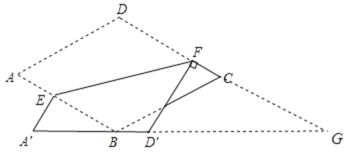
延长DC和![]() ,两延长线相交于点G,利用菱形的性质可证得∠A=∠DCB=60°,AB=BC=DC,利用折叠的性质可得到∠D=∠
,两延长线相交于点G,利用菱形的性质可证得∠A=∠DCB=60°,AB=BC=DC,利用折叠的性质可得到∠D=∠![]() F=120°,DF=
F=120°,DF=![]() F,再证明∠CBG=∠G=30°,利用等角对等边可得到BC=CG,设CF=x,DF=y,用含x,y的代数式表示出DC,CG,FG的长,然后在Rt△
F,再证明∠CBG=∠G=30°,利用等角对等边可得到BC=CG,设CF=x,DF=y,用含x,y的代数式表示出DC,CG,FG的长,然后在Rt△![]() FG中,利用解直角三角形可得到x与y的关系式,据此可求出CF与DF的比值.
FG中,利用解直角三角形可得到x与y的关系式,据此可求出CF与DF的比值.
解:延长DC和![]() ,两延长线相交于点G,
,两延长线相交于点G,
∵菱形ABCD,∠A=60°,
∴∠A=∠DCB=60°,AB=BC=DC
∴∠BCG=180°-60°=120°,
∵将纸片折叠,点A,D分别落在点![]() 处,且
处,且![]() 经过点B,EF为折痕,
经过点B,EF为折痕,
∴∠D=∠![]() F=120°,DF=
F=120°,DF=![]() F
F
∵![]() F⊥DC,
F⊥DC,
∴∠![]() FG=90°,
FG=90°,
∴∠G=90°-60°=30°
∴∠CBG=180°-∠G-∠BCG=180°-30°-120°=30°
∴∠CBG=∠G
∴BC=CG,
设CF=x,DF=y,则DC=CG=x+y
∴FG=2x+y,
在Rt△![]() FG中,
FG中,
![]()
![]()
![]()
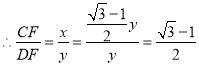 .
.
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目