题目内容
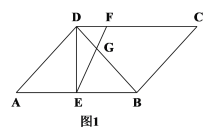
【题目】如图![]() ,在正方形
,在正方形![]() 中,
中,![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,连接
的中点,连接![]() 、
、![]() 交于点
交于点![]() .
.
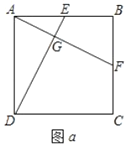
(1)求证:![]() ;
;
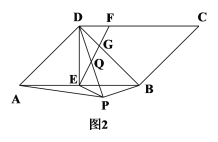
(2)如图![]() ,连接
,连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
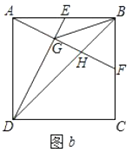
①求证:![]() ;
;
②若![]() ,求三角形
,求三角形![]() 的面积.
的面积.
【答案】(1)详见解析;(2)①详见解析;②![]()
【解析】
(1)由正方形的性质可得AD=BC=DC=AB,AE=BE=![]() AB,BF=CF=
AB,BF=CF=![]() BC,由SAS可证△ADE≌△BAF,可得∠BAF=∠ADE,由余角的性质可得结论;
BC,由SAS可证△ADE≌△BAF,可得∠BAF=∠ADE,由余角的性质可得结论;
(2)①过点B作BN⊥AF于N,由AAS可证△ABN≌△ADG,可得AG=BN,DG=GN,由平行线分线段成比例可得AG=GN,由勾股定理可得结论;
②由勾股定理可求DE的长,由面积法可求AG的长,由相似三角形的性质可求GH的长,由三角形的面积可求解.
解:(1)证明:∵正方形![]() ,
,![]() 、
、![]() 分别为边
分别为边![]() 、
、![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵在△ADE和△BAF中,
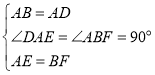 ,
,
∴△ADE和△BAF(SAS),
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)证明:①如图![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
在△ABN和△ADG中,
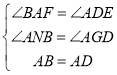 ,
,
∴△ABN和△ADG(AAS),
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
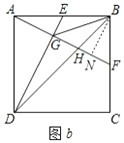
②∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
且![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】小明投资销售一种进价为每件20元的护眼台灯.经过市场调研发现,每月销售的数量y(件)是售价x(元/件)的一次函数,其对应关系如表:
x/(元/件) | 22 | 25 | 30 | 35 | … |
y/件 | 280 | 250 | 200 | 150 | … |
在销售过程中销售单价不低于成本价,物价局规定每件商品的利润不得高于成本价的60%,
(1)请求出y关于x的函数关系式.
(2)设小明每月获得利润为w(元),求每月获得利润w(元)与售价x(元/件)之间的函数关系式,并确定自变量x的取值范围.
(3)当售价定为多少元/件时,每月可获得最大利润,最大利润是多少?