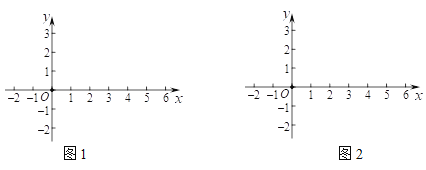题目内容
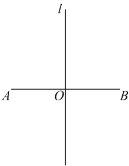
【题目】如图，点A，B，C为平面内不在同一直线上的三点．点D为平面内一个动点．线段AB，BC，CD，DA的中点分别为M，N，P，Q．在点D的运动过程中，有下列结论：①存在无数个中点四边形MNPQ是平行四边形；②存在无数个中点四边形MNPQ是菱形；③存在无数个中点四边形MNPQ是矩形；④存在两个中点四边形MNPQ是正方形．所有正确结论的序号是_____．
【答案】①②③④．
【解析】
连接AC、BD，根据三角形中位线定理得到PQ∥AC，PQ=
AC，MN∥AC，MN=AC，根据平行四边形、矩形、菱形、正方形的判定定理判断即可．
①当AC与BD不平行时，中点四边形MNPQ是平行四边形；
故存在无数个中点四边形MNPQ是平行四边形；
②当AC与BD相等且不平行时，中点四边形MNPQ是菱形；
故存在无数个中点四边形MNPQ是菱形；
③当AC与BD互相垂直（B，D不重合）时，中点四边形MNPQ是矩形；
故存在无数个中点四边形MNPQ是矩形；
④如图所示，当AC与BD相等且互相垂直时，中点四边形MNPQ是正方形．
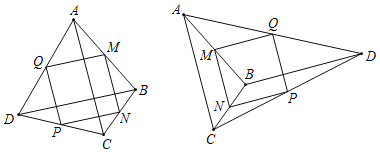
故存在两个中点四边形MNPQ是正方形．
故答案为：①②③④．
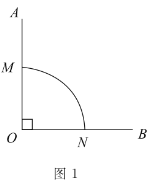
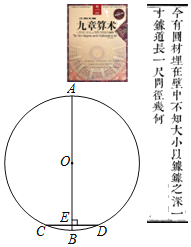
【题目】已知：如图，线段AB＝5cm，∠BAM＝90°，P是
与∠BAM所围成的图形的外部的一定点，C是上一动点，连接PC交弦AB于点D．设A，D两点间的距离为xcm，P，D两点间的距离为y1cm，P，C两点间的距离为y2cm．小腾根据学习函数的经验，分别对函数y1，y2随自变量x的变化而变化的规律进行了探究．
下面是小腾的探究过程，请补充完整：
按照表中自变量x的值进行取点、画图、测量，分别得到了y1，y2与x的几组对应值：
x/cm | 0.00 | 1.00 | 1.56 | 1.98 | 2.50 | 3.38 | 4.00 | 4.40 | 5.00 |
y1/cm | 2.75 | 3.24 | 3.61 | 3.92 | 4.32 | 5.06 | 5.60 | 5.95 | 6.50 |
y2/cm | 2.75 | 4.74 | 5.34 | 5.66 | 5.94 | 6.24 | 6.37 | 6.43 | 6.50 |
（1）在同一平面直角坐标系xOy中，画出各组数值所对应的点（x，y1），（x，y2），并画出函数y1，y2的图象；
（2）连接BP，结合函数图象，解决问题：当△BDP为等腰三角形时，x的值约为_____cm（结果保留一位小数）．
