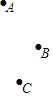题目内容
【题目】对于平面直角坐标系xOy中的任意点![]() ,如果满足
,如果满足![]() (x≥0,a为常数),那么我们称这样的点叫做“特征点”.
(x≥0,a为常数),那么我们称这样的点叫做“特征点”.
(1)当2≤a≤3时,
①在点![]() 中,满足此条件的特征点为__________________;
中,满足此条件的特征点为__________________;
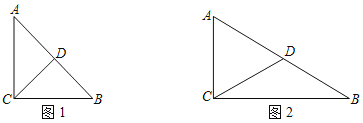
②⊙W的圆心为![]() ,半径为1,如果⊙W上始终存在满足条件的特征点,请画出示意图,并直接写出m的取值范围;
,半径为1,如果⊙W上始终存在满足条件的特征点,请画出示意图,并直接写出m的取值范围;
(2)已知函数![]() ,请利用特征点求出该函数的最小值.
,请利用特征点求出该函数的最小值.
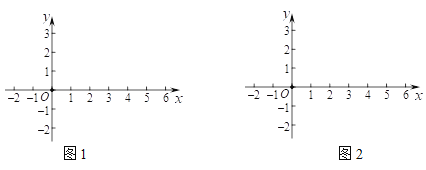
【答案】(1)①![]() ;②
;②![]() ;(2)最小值为2.
;(2)最小值为2.
【解析】
(1)①根据“特征点”的定义判断即可;
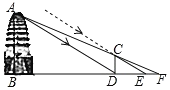
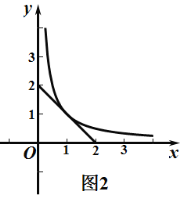
②如图2中,当⊙W1与直线y=x+2相切时,![]() ,当⊙W2与直线y=x+3相切时,
,当⊙W2与直线y=x+3相切时,![]() ,结合图象,⊙W与图中阴影部分有交点时,⊙W上存在满足条件的特征点.
,结合图象,⊙W与图中阴影部分有交点时,⊙W上存在满足条件的特征点.
(2)特征点的图象是由原点向外扩大,当与反比例函数的图象第一次有交点时,![]() 的值最小(如图3中).
的值最小(如图3中).
解:(1)①∵1+2=3,1+3=4,2.5+0=2.5,
又∵2≤a≤3,
∴A,C是特征点,
故答案为:![]() ;
;
②如图1,∵2≤a≤3,
∴直线y=x+2和直线y=x+3之间的区域(包括两直线)上的点都为“特征点”,
直线y=x+2和直线y=x+3分别与x轴的交点为![]() ,
,![]() ,
,
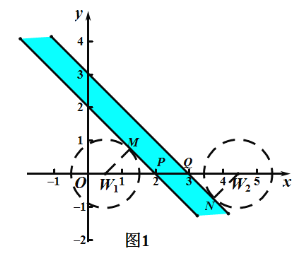
当⊙W1与直线y=x+2相切时,设切点为M,
此时![]() ,
,![]() ,
,![]() ,则
,则![]() 为等腰直角三角形,
为等腰直角三角形,
∵⊙W1半径为1,即![]() ,
,
∴![]() ,则
,则![]() ,
,
∴![]() ,
,
当⊙W2与直线y=x+3相切时,设切点为N,
此时![]() ,
,![]() ,
,![]() ,则
,则![]() 为等腰直角三角形,
为等腰直角三角形,
同理得:![]() ,则
,则![]() ,
,
∴![]() ,
,
观察图象可知满足条件的m取值范围为:![]() ;
;
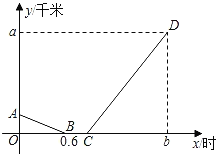
(2)根据![]() ,在第一象限画出
,在第一象限画出![]() 的图象,
的图象,
∴在此坐标系中图象上的点就是![]() ,
,
∵特征点满足![]() (x≥0,a为常数),
(x≥0,a为常数),
∴在此图象上对应的就是![]() ,
,
∴将特征点的图象由原点向外扩大,当与反比例函数![]() 的图象第一次有交点时,
的图象第一次有交点时,![]() 出现最小值,
出现最小值,
如图2,由x>0可将![]() 整理得:
整理得:![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,![]() (舍去),
(舍去),
∴![]() ,
,
∴![]() ,即
,即![]() 的最小值为2.
的最小值为2.

【题目】疫情期间,甲、乙、丙、丁4名同学约定周一至周五每天做一组俯卧撑.为了增加趣味性,他们通过游戏方式确定每个人每天的训练计划.
首先,按如图方式摆放五张卡片,正面标有不同的数字代表每天做俯卧撑的个数,反面标有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 便于记录.
便于记录.
![]()
具体游戏规则如下:
甲同学:同时翻开![]() ,
,![]() ,将两个数字进行比较,然后由小到大记录在表格中,
,将两个数字进行比较,然后由小到大记录在表格中,![]() ,
,![]() ,
,![]() 按原顺序记录在表格中;
按原顺序记录在表格中;
乙同学:同时翻开![]() ,
,![]() ,
,![]() ,将三个数字进行比较,然后由小到大记录在表格中,
,将三个数字进行比较,然后由小到大记录在表格中,![]() ,
,![]() 按原顺序记录在表格中;
按原顺序记录在表格中;
以此类推,到丁同学时,五张卡片全部翻开,并由小到大记录在表格中.
下表记录的是这四名同学五天的训练计划:
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | |
甲同学 |
|
|
|
|
|
乙同学 |
|
|
|
|
|
丙同学 | |||||
丁同学 |
|
|
|
|
|
根据记录结果解决问题:
(1)补全上表中丙同学的训练计划;
(2)已知每名同学每天至少做30个,五天最多做180个.
①如果![]() ,
,![]() ,那么
,那么![]() 所有可能取值为__________________________;
所有可能取值为__________________________;
②这四名同学星期_________做俯卧撑的总个数最多,总个数最多为_________个.
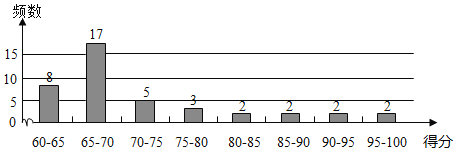
【题目】改革开放以来,人们的支付方式发生了巨大转变,近年来,移动支付已成为主要的支付方式之一,为了解某校学生上个月![]() 两种移动支付方式的使用情况,从全校
两种移动支付方式的使用情况,从全校![]() 名学生中随机抽取了
名学生中随机抽取了![]() 人,发现样本中
人,发现样本中![]() 两种支付方式都不使用的有
两种支付方式都不使用的有![]() 人,样本中仅使用
人,样本中仅使用![]() 种支付方式和仅使用
种支付方式和仅使用![]() 种支付方式的学生的支付金额
种支付方式的学生的支付金额![]() (元)的分布情况如下:
(元)的分布情况如下:
支付金额 支付方式 |
|
|
|
仅使用 |
|
|
|
仅使用 |
|
|
|
下面有四个推断:
①从样本中使用移动支付的学生中随机抽取一名学生,该生使用A支付方式的概率大于他使用B支付方式的概率;
②根据样本数据估计,全校1000名学生中.同时使用A、B两种支付方式的大约有400人;
③样本中仅使用A种支付方式的同学,上个月的支付金额的中位数一定不超过1000元;
④样本中仅使用B种支付方式的同学,上个月的支付金额的平均数一定不低于1000元.其中合理的是( )
A.①③B.②④C.①②③D.①②③④