题目内容
【题目】已知:在平面直角坐标系![]() 中,对于任意的实数
中,对于任意的实数![]() ,直线
,直线![]() 都经过平面内一个定点
都经过平面内一个定点![]() .
.
(1)求点![]() 的坐标.
的坐标.
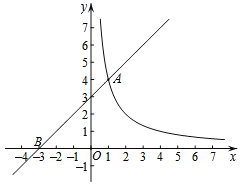
(2)反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() 和另外一点
和另外一点![]()
①求![]() 的值;
的值;
②当![]() 时,求
时,求![]() 的取值范围
的取值范围
【答案】(1) A(-1,-2);(2)①b=2, m>0或m<-1.
【解析】
(1)解析式化为y=ax+a-2=a(x+1)-2,即可求得;
(2)①根据待定系数法即可求得;②根据反比例函数的性质即可判定点P(m,n)在第一象限或第三象限两种情况,分别讨论即可.
解:(1)∵y=ax+a-2=a(x+1)-2,
∴当x=-1时,y=-2,
∴直线y=ax+a-2都经过平面内一个定点A(-1,-2);
故答案为:A(-1,-2).
(2)①∵反比例函数![]() 的图像经过点A,
的图像经过点A,
∴b=-1×(-2)=2;
②若点P(m,n)在第一象限,当n>-2时,m>0,
若点P(m,n)在第三象限,当n>-2时,m<-1,
综上,当n>-2时,m>0或m<-1.
故答案为:b=2,m的取值范围是:m>0或m<-1.

练习册系列答案
相关题目