Question

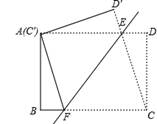
如图，将矩形ABCD沿直线EF折叠，使点C与点A重合，折痕交AD于点E，交BC于点F，连接AF，设AE=a，ED=b，DC=c，则下列关于a，b，c的关系式正确的是（　　）

A．a=b+c

B．a+b=2c

C．a2+c2=4b2

D．a2﹣b2=c2

Answer 1

D.

试题分析：本题考查的是翻折变换，涉及到矩形的性质、勾股定理等知识．此题难度适中，注意掌握数形结合思想的应用，注意折叠中的对应关系．∵四边形C′D′EF由四边形CDEF折叠而成，∴CE=AE，∵四边形ABCD是矩形，∴∠D=90°，∵AE=a，ED=b，DC=c，∴CE=AE=a，在Rt△DCE中，CE²=CD²+DE²，∴a、b、c三者之间的数量关系式为：a²=b²+c²，即a²-b²=c²．故选D．