Question

【题目】如图，直线 的解析式为，直线 的解析式为，为上的一点，且点的坐标为作直线 轴，交直线于 点，再作于点，交直线 于点，作轴，交直线于点，再作 于点，作轴，交直线于点....按此作法继续作下去，则 的坐标为_____，的坐标为______

Answer 1

【答案】

【解析】

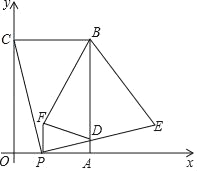
依据直角三角形“角所对直角边等于斜边的一半”求得B点的坐标，然后根据等腰三角形的性质，求得OB=BA1，最后根据平行于x轴的直线上两点纵坐标相等，即可求得A1的坐标，依此类推即可求得An的坐标．

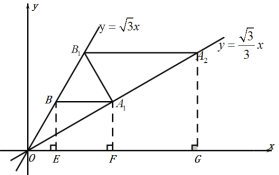
如图，作⊥轴于E，⊥轴于F，⊥轴于G，

∵点的坐标为，

∴，，

∴ ，

∴，

∴，，

∵∥轴，
根据平行于轴的直线上两点纵坐标相等，

∴的纵坐标为，

∵点在直线上，

将代入得，解得：，

∴的坐标为，

∴，，

∴，

∴，

∴，

∴，

∵∥轴，，

∴，

根据等腰三角形三线合一的性质知：

，

∴，

∴，

，

∴的坐标为，

同理可得：的坐标为，