题目内容
【题目】如图,隧道的截面由抛物线ADC和矩形AOBC构成,矩形的长OB是12m,宽OA是4m.拱顶D到地面OB的距离是10m.若以O原点,OB所在的直线为x轴,OA所在的直线为y轴,建立直角坐标系.
(1)画出直角坐标系xOy,并求出抛物线ADC的函数表达式;
(2)在抛物线型拱壁E、F处安装两盏灯,它们离地面OB的高度都是8m,则这两盏灯的水平距离EF是多少米?

【答案】(1)画直角坐标系xOy见解析,抛物线ADC的函数表达式为:y=﹣![]() (x﹣6)2+10;
(x﹣6)2+10;
(2)两盏灯的水平距离EF是4![]() 米.
米.
【解析】试题分析:
(1)按照题中要求画出对应的坐标系;则由题意可得抛物线ADC的顶点坐标为(6,10),A点坐标为(0,4),由此即可用“待定系数法”求出抛物线的解析式;
(2)在(1)中所求的抛物线的解析式中,由![]() 可得对应的一元二次方程,解方程即可得到点E、F的横坐标,由此即可求得EF的长;
可得对应的一元二次方程,解方程即可得到点E、F的横坐标,由此即可求得EF的长;
试题解析:
解:(1)画出直角坐标系xOy,如图:
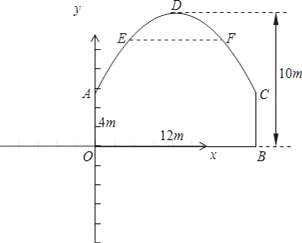
由题意可知,抛物线ADC的顶点坐标为(6,10),A点坐标为(0,4),
可设抛物线ADC的函数表达式为y=a(x﹣6)2+10,
将x=0,y=4代入得:a=![]() ,
,
∴抛物线ADC的函数表达式为:y=![]() (x﹣6)2+10.
(x﹣6)2+10.
(2)由y=8得: ![]() (x﹣6)2+10=8,
(x﹣6)2+10=8,
解得:x1=6+![]() ,x2=6﹣
,x2=6﹣![]() ,
,
则EF=x1﹣x2=![]() ,即两盏灯的水平距离EF是
,即两盏灯的水平距离EF是![]() 米.
米.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目