题目内容
【题目】如图，这是一个供滑板爱好者使用的
型池的示意图，该型池可以看成是长方体去掉一个“半圆柱”而成，中间可供滑行部分的截面是直径为
的半圆，其边缘
，点
在
上，
，一滑板爱好者从
点滑到点，则他滑行的最短距离约为_________
．（边缘部分的厚度忽略不计）
【答案】25
【解析】
滑行的距离最短，即是沿着AE的线段滑行，我们可将半圆展开为矩形来研究，展开后，A、D、E三点构成直角三角形，AE为斜边，AD和DE为直角边，写出AD和DE的长，根据题意，写出勾股定理等式，代入数据即可得出AE的距离．
将半圆面展开可得：
AD=
米，DE=DC-CE=AB-CE=20-5=15米，
在Rt△ADE中，
米，
即滑行的最短距离为25米，
故答案为：25.
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
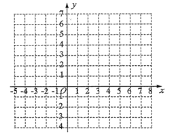
【题目】已知二元一次方程
，通过列举将方程的解写成下列表格的形式：
| -1 |
|
| 5 | 6 |
| 6 | 5 |
| 0 |
|
如果将二元一次方程的解所包含的未知数
的值对应直角坐标系中一个点的横坐标，未知数
的值对应这个点的纵坐标，这样每一个二元一次方程的解，就可以对应直角坐标系中的一个点，例如：方程的解
的对应点是
．
（1）表格中的
________，
___________；
（2）通过以上确定对应点坐标的方法，将表格中给出的五个解依次转化为对应点的坐标，并在所给的直角坐标系中画出这五个点；根据这些点猜想方程的解的对应点所组成的图形是_________，并写出它的两个特征①__________，②_____________；
（3）若点
好落在的解对应的点组成的图形上，求
的值．
