Question

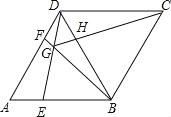
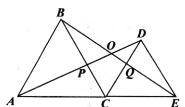
【题目】如图，点为线段上一点，在同侧分别作正三角形和，分别与、交于点、，与交于点，以下结论：①≌；②；③；④．以上结论正确的有_________（把你认为正确的序号都填上）．

Answer 1

【答案】①②④

【解析】

根据等边三角形的性质可得CA=CB，CD=CE，∠ACB=∠DCE=60°，然后根据等式的基本性质可得∠ACD=∠BCE，利用SAS即可证出≌，即可判断①；根据全等三角形的性质，即可判断②；利用三角形的内角和定理和等量代换即可求出∠AOB，即可判断③，最后利用ASA证出≌，即可判断④．

解：∵△ABC和△CDE都是等边三角形

∴CA=CB，CD=CE，∠ACB=∠DCE=60°

∴∠ACB＋∠BCD=∠DCE＋∠BCD

∴∠ACD=∠BCE

在和中

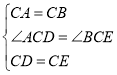
∴≌，故①正确；

∴∠CAD=∠CBE，，故②正确；

∵∠OPB=∠CPA

∴∠AOB=180°－∠OPB－∠CBE=180°－∠CPA－∠CAD=∠ACB=60°，故③错误；

∵∠BCQ=180°－∠ACB－∠DCE=60°

∴∠ACP=∠BCQ

在和中

∴≌，

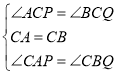
∴，故④正确．

故答案为：①②④．