题目内容
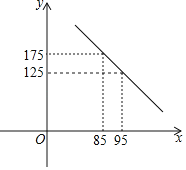
【题目】武汉“新冠肺炎”发生以来,某医疗公司积极复工,加班加点生产医用防护服,为防控一线助力.以下是该公司以往的市场调查,发现该公司防护服的日销售量y(套)与销售单价x(元)之间满足一次函数关系,如下图所示,关于日销售利润w(元)和销售单价x(元)的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 |
日销售利润w(元) | 875 | 1875 | 1875 |
(注:日销售利润=日销售量×(销售单价一成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围);
(2)根据函数图象和表格所提供的信息,填空:
该公司生产的防护服的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)该公司复工以后,在政府部门的帮助下,原材料采购成本比以往有了下降,平均起来,每生产一套防护服,成本比以前下降5元.该公司计划开展科技创新,以降低该产品的成本,如果在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
【答案】(1)y=﹣5x+600(80≤x≤120);(2)80,100,2000;(3)产品的成本单价应不超过65元.
【解析】
(1)设y与x之间的函数解析式为:y=kx+b,根据函数图象,利用待定系数法确定函数关系式即可;
(2)设成本单价是a元,根据日销售利润=日销售量×(销售单价一成本单价),代入表格数据进行计算求得成本单价,然后得到利润w与销量x的关系,利用完全平方公式变形即可得解;
(3)设产品的成本单价为b元,根据题意列出关于b的不等式,然后求解即可.
(1)设y与x之间的函数解析式为:y=kx+b,
由题意得,![]() ,
,
解得:![]() ,
,
∴y与x之间的函数解析式为y=﹣5x+600(80≤x≤120);
(2)设成本单价是a元,
由题意得,(﹣5×85+600)×(85﹣a)=875,
解得:a=80,
∴该公司生产的防护服的成本单价是80元;
∵w=(﹣5x+600)(x﹣a)=﹣5x2+(600+5a)x﹣600a=﹣5(x﹣100)2+2000,
∴当x=100时,W最大=2000,
即每件销售单价为100元时,每天的销售利润最大,最大利润是2000;
故答案为:80,100,2000;
(3)设产品的成本单价为b元,
当x=90时,(﹣5×90+600)(90﹣b)≥3750,
解得:b≤65,
答:产品的成本单价应不超过65元.

 阅读快车系列答案
阅读快车系列答案