Question

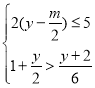【题目】若关于x的分式方程﹣=3的解为正整数，且关于y的不等式组至多有六个整数解，则符合条件的所有整数m的取值之和为（　　）

A.1B.0C.5D.6

Answer 1

【答案】A

【解析】

先求出一元一次不等式组的解集，根据“不等式组的解至多有六个整数解”确定m的取值范围，再解分式方程，依据“解为正整数”进一步确定m的值，最后求和即可．

解：化简不等式组为，

解得：﹣2＜y≤，

∵不等式组至多有六个整数解，

∴≤4，

∴m≤3，

将分式方程的两边同时乘以x﹣2，得

x+m﹣1=3（x﹣2），

解得：x=，

∵分式方程的解为正整数，

∴m+5是2的倍数，

∵m≤3，

∴m=﹣3或m=﹣1或m=1或m=3，

∵x≠2，

∴≠2，

∴m≠﹣1，

∴m=﹣3或m=1或m=3，

∴符合条件的所有整数m的取值之和为1，

故选：A．