题目内容
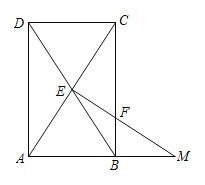
【题目】如图,在矩形ABCD中,AB=3,BC=4,点E为射线CB上一动点(不与点C重合),将△CDE沿DE所在直线折叠,点C落在点C′处,连接AC′,当△AC′D为直角三角形时,CE的长为_____.
【答案】4﹣![]() 或4+
或4+![]()
【解析】
由折叠的性质得:C'D=CD=3,C'E=CE,∠DC'E=∠C=90°,设CE=C'E=x,分点C'在矩形内与矩形外两种情况,如图1,在△AC'D利用勾股定理求得AC'的长,在 Rt△ABE中,利用勾股定理得到关于x的方程,然后求解方程即可;如图2,同理1进行求解即可.
∵四边形ABCD是矩形,
∴∠B=∠C=90°,AD=BC=4,CD=AB=3,
由折叠的性质得:C'D=CD=3,C'E=CE,∠DC'E=∠C=90°,
设CE=C'E=x,
当△AC′D为直角三角形时,则∠AC'D=90°,
∴∠AC'D+∠DC'E=180°,
∴A、C'、E三点共线,
分两种情况:
①点E在线段CB上时,如图1所示:
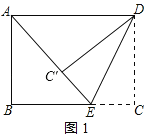
则∠DC'E=∠C=90°,
∴∠AC'D=90°,
∴AC'=![]() ,
,
在Rt△ABE中,BE=4﹣x,AE=x+![]() ,
,
由勾股定理得:(4﹣x)2+32=(x+![]() )2,
)2,
解得:x=4﹣![]() ,
,
∴CE=4﹣![]() ;
;
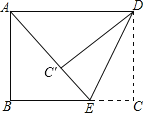
②点E在线段CB的延长线上时,如图2所示:

则∠DC'E=∠C=90°,
∴AC'=![]() ,
,
在Rt△ABE中,BE=x﹣4,AE=x﹣![]() ,
,
由勾股定理得:(x﹣4)2+32=(x﹣![]() )2,
)2,
解得:x=4+![]() ,
,
∴CE=4+![]() ;
;
综上所述,当△AC′D为直角三角形时,CE的长为4﹣![]() 或4+
或4+![]() ;
;
故答案为:4﹣![]() 或4+
或4+![]() .
.

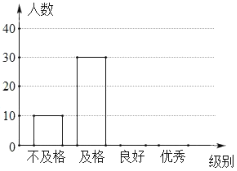
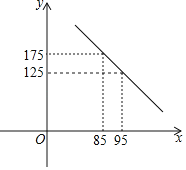
【题目】武汉“新冠肺炎”发生以来,某医疗公司积极复工,加班加点生产医用防护服,为防控一线助力.以下是该公司以往的市场调查,发现该公司防护服的日销售量y(套)与销售单价x(元)之间满足一次函数关系,如下图所示,关于日销售利润w(元)和销售单价x(元)的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 |
日销售利润w(元) | 875 | 1875 | 1875 |
(注:日销售利润=日销售量×(销售单价一成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围);
(2)根据函数图象和表格所提供的信息,填空:
该公司生产的防护服的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)该公司复工以后,在政府部门的帮助下,原材料采购成本比以往有了下降,平均起来,每生产一套防护服,成本比以前下降5元.该公司计划开展科技创新,以降低该产品的成本,如果在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
【题目】![]() ,
,![]() 两地相距
两地相距![]() ,甲、乙两人都由
,甲、乙两人都由![]() 地去
地去![]() 地,甲骑自行车,平均速度为
地,甲骑自行车,平均速度为![]() ;乙乘汽车,平均速度为
;乙乘汽车,平均速度为![]() ,且比甲晚
,且比甲晚![]() 出发.设甲的骑行时间为
出发.设甲的骑行时间为![]()
![]() .
.
(1)根据题意,填写表格:
时间 与 | 0.5 | 1.8 | |
甲与 | 5 | 20 | |
乙与 | 0 | 12 |
(2)设甲,乙两人与![]() 地的距离为
地的距离为![]() 和
和![]() .写出
.写出![]() ,
,![]() 关于
关于![]() 的表达式;
的表达式;
(3)设甲,乙两人之间的距离为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.