Question

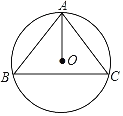
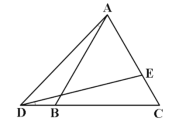
【题目】如图，等边三角形中，，点D是延长线上一点，且，点E在直线上，当时，的长为_____.

Answer 1

【答案】2或.

【解析】

分①在线段AC上，②在线段AC的延长线上两种情况讨论.对于①作EF//AB与BC相交于F，证明△DFE∽△ABD，利用相似三角形对应边相等可求得EC，即也可求得AE；对于②作EF//AB与BC的延长线交于F，证明△DCE∽△ABD，利用相似三角形对应边相等可求得EC，即也可求得AE.

解：E点的位置有两种可能，①在线段AC上，②在线段AC的延长线上. E不可能在CA的延长线上（因为若E在CA的延长线上由①可知不可能等于）.

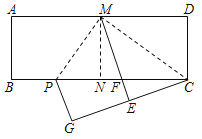
①若E在线段AC上，如图作EF//AB与BC相交于F，

∵为等边三角形，，

∴AC=BC=AB=3，，

∴∠ABD=120°，

∵EF//AB，

∴，

∴△EFC为等边三角形，∠EFD=120°，设EF=FC=EC=x.

∵，∠ABD=∠EFD=120°，

∴△DFE∽△ABD，

∴

∵，

∴

∴，解得

∴EF=FC=EC=1，

∴AE=AC-EC=3-1=2；

②若E点在线段AC的延长线上，作EF//AB与BC的延长线交于F.

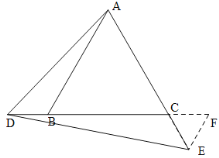
与①同理可证△EFC为等边三角形，∠ECD=120°，设EF=FC=EC=x.

∵，∠ABD=∠ECD=120°，

∴△DCE∽△ABD，

∴，

∵，

∴BD=BC+BD=4，

∴，解得，

∴EF=FC=EC=，

，

故答案为：2或.