题目内容
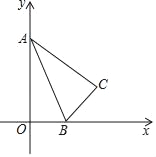
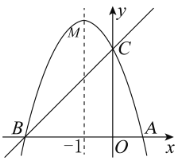
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
【答案】(1)抛物线的解析式为![]() ,直线的解析式为
,直线的解析式为![]() .(2)
.(2)![]() ;(3)
;(3)![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先把点A,C的坐标分别代入抛物线解析式得到a和b,c的关系式,再根据抛物线的对称轴方程可得a和b的关系,再联立得到方程组,解方程组,求出a,b,c的值即可得到抛物线解析式;把B、C两点的坐标代入直线y=mx+n,解方程组求出m和n的值即可得到直线解析式;
(2)设直线BC与对称轴x=-1的交点为M,此时MA+MC的值最小.把x=-1代入直线y=x+3得y的值,即可求出点M坐标;
(3)设P(-1,t),又因为B(-3,0),C(0,3),所以可得BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,再分三种情况分别讨论求出符合题意t值即可求出点P的坐标.
(1)依题意得: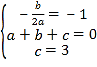 ,解得:
,解得: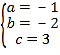 ,
,
∴抛物线的解析式为![]() .
.
∵对称轴为![]() ,且抛物线经过
,且抛物线经过![]() ,
,
∴把![]() 、
、![]() 分别代入直线
分别代入直线![]() ,
,
得![]() ,解之得:
,解之得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
(2)直线![]() 与对称轴
与对称轴![]() 的交点为
的交点为![]() ,则此时
,则此时![]() 的值最小,把
的值最小,把![]() 代入直线
代入直线![]() 得
得![]() ,
,
∴![]() .即当点
.即当点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小时
的距离之和最小时![]() 的坐标为
的坐标为![]() .
.
(注:本题只求![]() 坐标没说要求证明为何此时
坐标没说要求证明为何此时![]() 的值最小,所以答案未证明
的值最小,所以答案未证明![]() 的值最小的原因).
的值最小的原因).
(3)设![]() ,又
,又![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
①若点![]() 为直角顶点,则
为直角顶点,则![]() ,即:
,即:![]() 解得:
解得:![]() ,
,
②若点![]() 为直角顶点,则
为直角顶点,则![]() ,即:
,即:![]() 解得:
解得:![]() ,
,
③若点![]() 为直角顶点,则
为直角顶点,则![]() ,即:
,即:![]() 解得:
解得:
![]() ,
,![]() .
.
综上所述![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目