题目内容
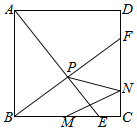
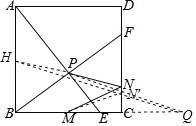
【题目】如图,正方形ABCD的边长为2,点E,点F分别是边BC,边CD上的动点,且BE=CF,AE与BF相交于点P.若点M为边BC的中点,点N为边CD上任意一点,则MN+PN的最小值等于_____.
【答案】![]()
【解析】
作M关于CD的对称点Q,取AB的中点H,连接PQ与CD交于点N',连接PH,HQ,当H、P、N'、Q四点共线时,MN+NP=PQ的值最小,根据勾股定理HQ,再证明△ABE≌△BCF,进而得△APB为直角三角形,由直角三角形的性质,求得PH,进而求得PQ.
解:作M关于CD的对称点Q,取AB的中点H,连接PQ与CD交于点N',连接PH,HQ,则MN'=QN',
∵四边形ABCD是正方形,
∴AB=BC,AB∥CD,∠ABC=∠BCD=90°,
在△ABE和△BCF中,
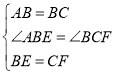 ,
,
∴△ABE≌△BCF(SAS),
∴∠AEB=∠BFC,
∵AB∥CD,
∴∠ABP=∠BFC=∠AEB,
∵∠BAE+∠AEB=90°,
∴∠BAE+∠ABP=90°,
∴∠APB=90°,
∴PH=![]() ,
,
∵M点是BC的中点,
∴BM=MC=CQ=![]() ,
,
∵PH+PQ≥HQ,
∴当H、P、Q三点共线时,PH+PQ=HQ=![]() 的值最小,
的值最小,
∴PQ的最小值为![]() ,
,
此时,若N与N'重合时,MN+PN=MN'+PN'=QN'+PN'=PQ=![]() 的值最小,
的值最小,
故答案为![]() .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目