Question

【题目】在平面上，对于给定的线段AB和点C，若平面上的点P（可以与点C重合）满足，∠APB＝∠ACB．则称点P为点C关于直线AB的联络点．

在平面直角坐标系xOy中，已知点A（2，0），B（0，2），C（﹣2，0）．

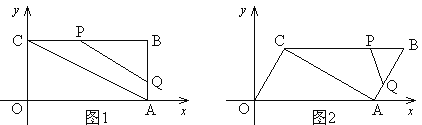
（1）在P1（2，2），P（1，0），R（1+，1）三个点中，是点O关于线段AB的联络点的是　 　．

（2）若点P既是点O关于线段AB的联络点，同时又是点B关于线段OA的联络点，求点P的横坐标m的取值范围；

（3）直线y＝x+b（b＞0）与x轴，y轴分交于点M，N，若在线段BC上存在点N关于线段OM的联络点，直接写出b的取值范围．

Answer 1

【答案】（1）P1，R．（2）1﹣≤m≤1+；（3）1≤b≤2．

【解析】

（1）根据点P为点C关于直线AB的联络点的定义一一判断即可．

（2）如图2中，作△AOB的外接圆⊙E，过点E作x轴的平行线交⊙E于G，H．首先说明当点P在优弧上时，点P既是点O关于线段AB的联络点，同时又是点B关于线段OA的联络点，求出G，H的坐标即可解决问题．

（3）如图3中，作△MON的外接圆⊙E，作点E关于X轴的对称点E′，以E′为圆心，OE′为半径作⊙E′．观察图象可知满足条件的点P在两个圆的优弧OM上，当⊙E与AB相切时，切点为H，求出点H的坐标即可判断．

解：（1）如图1中，

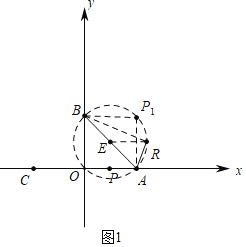
∵A（2，0），B（0，2），P1（2，2），P（1，0），R（1+，1），

∴OA＝OB＝AP1＝BP1，

∴四边形OAP1B是菱形，

∵∠AOB＝90°，

∴四边形OAP1B是正方形，

∴∠AP1B＝∠AOB＝90°，

∴P1是点O关于线段AB的联络点，

∵AB＝2，取AB的中点E（1，1），

∵ER＝＝BE＝AE，

∴∠ARB＝90°＝∠AOB，

∴点R是点O关于线段AB的联络点，

故答案为P1，R．

（2）如图2中，作△AOB的外接圆⊙E，过点E作x轴的平行线交⊙E于G，H．

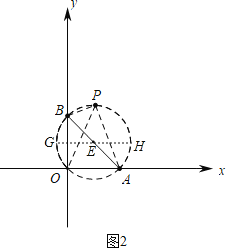
∵∠APB＝∠AOB＝90°，∠APO＝∠ABO＝45°，

∴当点P在优弧上时，点P既是点O关于线段AB的联络点，同时又是点B关于线段OA的联络点，

∵AB＝2，E（1，1），G（1﹣，1），H（1+，1）

∴点P的横坐标m的取值范围1﹣≤m≤1+．

（3）如图3中，作△MON的外接圆⊙E，作点E关于X轴的对称点E′，以E′为圆心，OE′为半径作⊙E′．

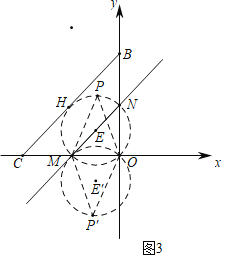
观察图象可知满足条件的点P在两个圆的优弧OM上，

当⊙E与AB相切时，切点为H，由题意⊙E的直径为，

∴MN＝，

∵OM＝ON，∠MON＝90°，

∴ON＝1，此时直线MN的解析式为y＝x+1，

观察图象可知：若在线段BC上存在点N关于线段OM的联络点，则b的取值范围为1≤b≤2.