题目内容
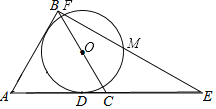
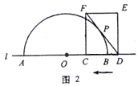
【题目】如图,等边△ABC与等腰三角形△EDC有公共顶点C,其中∠EDC=120°,AB=CE=2![]() ,连接BE,P为BE的中点,连接PD、AD
,连接BE,P为BE的中点,连接PD、AD
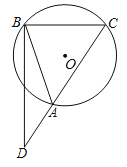
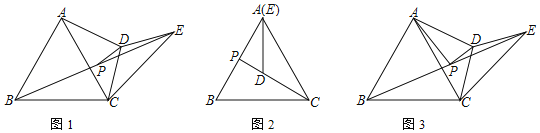
(1)为了研究线段AD与PD的数量关系,将图1中的△EDC绕点C旋转一个适当的角度,使CE与CA重合,如图2,请直接写出AD与PD的数量关系;
(2)如图1,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
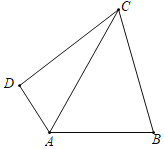
(3)如图3,若∠ACD=45°,求△ACD的面积.
【答案】(1)AD=2PD;(2)成立,理由见解析;(3)![]()
【解析】
(1)利用直角三角形30度角的性质即可解决问题.
(2)结论成立.如图1中,延长ED到F,使得DF=DE,连接BF,CF.利用三角形的中位线定理证明BF=2PD,再证明AD=BF即可解决问题.
(3)如图1中,延长BF交AD于G,由(2)得到∠FBC=∠DAC,首先证明∠ADP=60°,解直角三角形求出AD2即可解决问题.
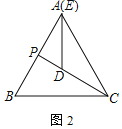
(1)如图2中,
等边△ABC中,∠BAC=60°,
等腰三角形△EDC中,∠ADC=120°,
∴∠DAC=∠CAD=30°,
∴∠DAP=∠BAC -∠DAC=30°,
∠PDA=180![]() -∠ADC=60°,
-∠ADC=60°,
∴∠APD=90°,
∴在Rt△APD中, AD=2PD;
(2)结论成立.
理由:如图1中,延长ED到F,使得DF=DE,连接BF,CF.
∵BP=EP,DE=DF,
∴BF=2PD,BF∥PD,
∵∠EDC=120°,
∴∠FDC=60°,
∵DF=DE=DC,
∴△DFC是等边三角形,
∵CB=CA,∠BCA=∠DCF=60°,
∴∠BCF+∠ACF =∠ACD+∠ACF=60°,
∴∠BCF=∠ACD,
∵CF=CD,
∴△BCF≌△ACD(SAS),
∴BF=AD,
∴AD=2PD.
(3)如图3中,作DM⊥AC于M, DG⊥EC于G.

在等腰△CDE中,
∵CE=2![]() ,∠CDE=120°,CD=DE,
,∠CDE=120°,CD=DE,
∴CG=GE=![]() ,∠DCE=30°,
,∠DCE=30°,
∴CD=DE=![]() 2
2![]() ,
,
∵∠ACD=45°,
∴CM=DM=2,
S△CAD=![]() .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案