题目内容
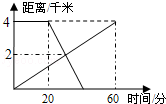
如图,已知直线 与x轴、y轴分别交于点A、B,线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.
与x轴、y轴分别交于点A、B,线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.

(1)求△AOB的面积;
(2)求点C坐标;
(3)点P是x轴上的一个动点,设P(x,0)
①请用x的代数式表示PB2、PC2;
②是否存在这样的点P,使得|PC-PB|的值最大?如果不存在,请说明理由;
如果存在,请求出点P的坐标.
 与x轴、y轴分别交于点A、B,线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.
与x轴、y轴分别交于点A、B,线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.
(1)求△AOB的面积;
(2)求点C坐标;
(3)点P是x轴上的一个动点,设P(x,0)
①请用x的代数式表示PB2、PC2;
②是否存在这样的点P,使得|PC-PB|的值最大?如果不存在,请说明理由;
如果存在,请求出点P的坐标.
(1)6;(2)(7,4);(3)①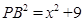 ,
,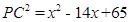 ;②存在这样的P点,P(3,0).
;②存在这样的P点,P(3,0).
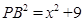 ,
,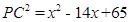 ;②存在这样的P点,P(3,0).
;②存在这样的P点,P(3,0).试题分析:(1)先由直线
 求出A、B两点的横坐标,即OA、OB的长,从而可求出△AOB的面积;
求出A、B两点的横坐标,即OA、OB的长,从而可求出△AOB的面积;(2)过C点作CD⊥x轴,垂足为D,构造Rt△ADC.易证△OAB≌△DCA,从而可求出CD=4,OD=7,所以C点坐标为(7,4);
(3)①由(2)可知,PD=7-x,在Rt△OPB中,
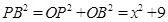 ,Rt△PCD中,
,Rt△PCD中,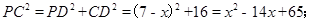
②存在这样的P点.P(3,0).
试题解析:(1)由直线
 ,令y=0,得OA=x=4,令x=0,得OB=y=3,∴S△AOB=
,令y=0,得OA=x=4,令x=0,得OB=y=3,∴S△AOB=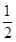 ×4×3=6;
×4×3=6;(2)过C点作CD⊥x轴,垂足为D,
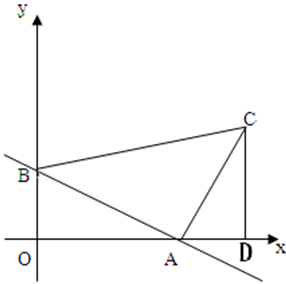
∵∠BAO+∠CAD=90°,∠ACD+∠CAD=90°,
∴∠BAO=∠ACD,
又∵AB=AC,∠AOB=∠CDA=90°,
∴△OAB≌△DCA,
∴CD=OA=4,AD=OB=3,则OD=4+3=7,
∴C(7,4);
(3)①由(2)可知,PD=7-x,
在Rt△OPB中,PB2=OP2+OB2=x2+9,
Rt△PCD中,PC2=PD2+CD2=(7-x)2+16=x2-14x+65,
②存在这样的P点.
设B点关于 x轴对称的点为B′,则B′(0,-3),
连接CB′,设直线B′C解析式为y=kx+b,将B′、C两点坐标代入,得
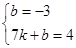 解得
解得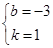
所以,直线B′C解析式为y=x-3,
令y=0,得P(3,0),此时|PC-PB|的值最大,

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目


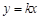 的图象经过点(-2,1),那么k 的值等于 .
的图象经过点(-2,1),那么k 的值等于 .