题目内容
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA.

(1)求△OAB的面积;
(2)若抛物线y=-x2-2x+c经过点A.
①求c的值;
②将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围(直接写出答案即可).

(1)求△OAB的面积;
(2)若抛物线y=-x2-2x+c经过点A.
①求c的值;
②将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围(直接写出答案即可).
(1)4 (2)①c=4 ②1<m<3
(1)根据点A的坐标是(-2,4),得出AB,BO的长度,即可得出△OAB的面积;
(2)①把点A的坐标(-2,4)代入y=-x2-2x+c中,直接得出即可;
②利用配方法求出二次函数解析式即可得出顶点坐标,根据AB的中点E的坐标以及F点的坐标即可得出m的取值范围.
解:(1)∵点A的坐标是(-2,4),AB⊥y轴,
∴AB=2,OB=4,
∴△OAB的面积为: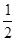 ×AB×OB=
×AB×OB=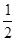 ×2×4=4,
×2×4=4,
(2)①把点A的坐标(-2,4)代入y=-x2-2x+c中,
-(-2)2-2×(-2)+c=4,
∴c=4,
②∵y=-x2-2x+4=-(x+1)2+5,
∴抛物线顶点D的坐标是(-1,5),
过点D作DE⊥AB于点E交AO于点F,
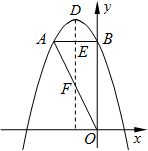
AB的中点E的坐标是(-1,4),OA的中点F的坐标是(-1,2),
∴m的取值范围是:1<m<3.
(2)①把点A的坐标(-2,4)代入y=-x2-2x+c中,直接得出即可;
②利用配方法求出二次函数解析式即可得出顶点坐标,根据AB的中点E的坐标以及F点的坐标即可得出m的取值范围.
解:(1)∵点A的坐标是(-2,4),AB⊥y轴,
∴AB=2,OB=4,
∴△OAB的面积为:
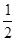 ×AB×OB=
×AB×OB=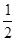 ×2×4=4,
×2×4=4,(2)①把点A的坐标(-2,4)代入y=-x2-2x+c中,
-(-2)2-2×(-2)+c=4,
∴c=4,
②∵y=-x2-2x+4=-(x+1)2+5,
∴抛物线顶点D的坐标是(-1,5),
过点D作DE⊥AB于点E交AO于点F,
AB的中点E的坐标是(-1,4),OA的中点F的坐标是(-1,2),
∴m的取值范围是:1<m<3.

练习册系列答案
相关题目
 的图象过点C(0,1),顶点为Q(2,3)点D在x轴正半轴上,且线段OD=OC
的图象过点C(0,1),顶点为Q(2,3)点D在x轴正半轴上,且线段OD=OC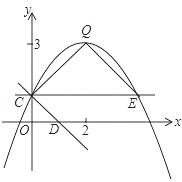
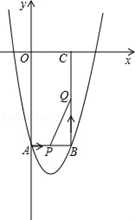
 ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.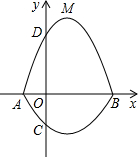
 .
. 米,在如图所示的坐标系中,这个喷泉的函数关系式是( )
米,在如图所示的坐标系中,这个喷泉的函数关系式是( )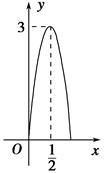
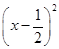 +3
+3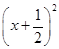 +3
+3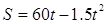 ,则飞机着陆后滑行 米才能停下来。
,则飞机着陆后滑行 米才能停下来。 的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成
的最小值”提出各自的想法.甲说:“可以利用已经学过的完全平方公式,把它配方成 ,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成
,所以代数式的最小值为-2”.乙说:“我也用配方法,但我配成 ,最小值为2”.你认为( )
,最小值为2”.你认为( )