题目内容
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组成一条封闭曲线,我们把这条封闭曲线称为“蛋线”,已知点C的坐标为(0,-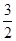 ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
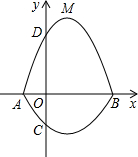
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限内是否存在一点P,使得∆PBC的面积最大?若存在,求出∆PBC面积的最大值;若不存在,请说明理由;
(3)当∆BDM为直角三角形时,请直接写出m的值.(参考公式:在平面直角坐标系中,若M(x1,y1),N(x2,y2),则M、N两点间的距离为MN=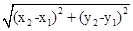 .
.
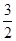 ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.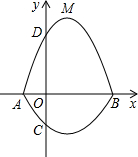
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限内是否存在一点P,使得∆PBC的面积最大?若存在,求出∆PBC面积的最大值;若不存在,请说明理由;
(3)当∆BDM为直角三角形时,请直接写出m的值.(参考公式:在平面直角坐标系中,若M(x1,y1),N(x2,y2),则M、N两点间的距离为MN=
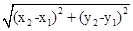 .
.(1)A(-1,0),B(3,0);(2)存在,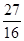 ;(3)-1或-
;(3)-1或-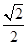 .
.
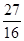 ;(3)-1或-
;(3)-1或-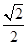 .
.试题分析:(1)将y=mx2-2mx-3m化为交点式,即可得到A、B两点的坐标;
(2)先用待定系数法得到抛物线C1的解析式,过点P作PQ∥y轴,交BC于Q,用待定系数法得到直线BC的解析式,再根据三角形的面积公式和配方法得到△PBC面积的最大值;
(3)先表示出DM2,BD2,MB2,再分两种情况:①DM2+BD2=MB2时;②DM2+MB2=BD2时,讨论即可求得m的值.
试题解析:(1)y=mx2-2mx-3m=m(x-3)(x+1),
∵m≠0,
∴当y=0时,x1=-1,x2=3,
∴A(-1,0),B(3,0);
(2)设C1:y=ax2+bx+c,将A、B、C三点的坐标代入得:
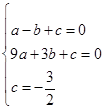 ,解得
,解得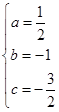 ,
,故C1:y=
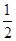 x2-x-
x2-x-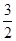 .
.依题意,设点P的坐标为(n,
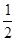 n2-n-
n2-n-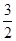 )(0<n<3)
)(0<n<3)则S∆PBC=S∆POC+S∆BOP-S∆BOC =
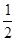 ×
×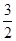 ×n+
×n+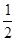 ×3×(-
×3×(-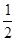 n2+n+
n2+n+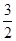 )-
)-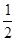 ×3×
×3×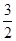
=-
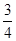 (n-
(n-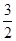 )2+
)2+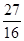
∵-
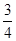 <0,
<0,∴当n=
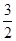 时S∆PBC的最大值是
时S∆PBC的最大值是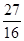
(3)y=mx2-2mx-3m=m(x-1)2-4m,顶点M坐标(1,-4m),
当x=0时,y=-3m,
∴D(0,-3m),B(3,0),
∴DM2=(0-1)2+(-3m+4m)2=m2+1,
MB2=(3-1)2+(0+4m)2=16m2+4,
BD2=(3-0)2+(0+3m)2=9m2+9,
当△BDM为Rt△时有:DM2+BD2=MB2或DM2+MB2=BD2.
①DM2+BD2=MB2时有:m2+1+9m2+9=16m2+4,
解得m=-1(∵m<0,∴m=1舍去);
②DM2+MB2=BD2时有:m2+1+16m2+4=9m2+9,
解得m=-
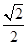 (m=
(m=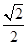 舍去).
舍去).综上,m=-1或-
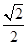 时,△BDM为直角三角形.
时,△BDM为直角三角形.考点: 二次函数综合题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
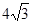 时,求x的值.
时,求x的值.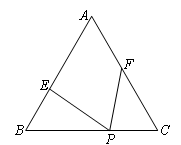
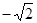 x2+mx+n的图象经过A,C两点.
x2+mx+n的图象经过A,C两点.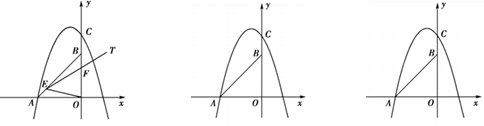
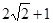 )倍.若存在,请直接写出点P坐标;若不存在,请说明理由.
)倍.若存在,请直接写出点P坐标;若不存在,请说明理由.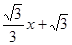 与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点
与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点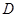 是劣弧AO上一动点(
是劣弧AO上一动点(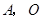 不重合).抛物线y=-
不重合).抛物线y=-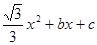 经过点A、C,与x轴交于另一点B,
经过点A、C,与x轴交于另一点B,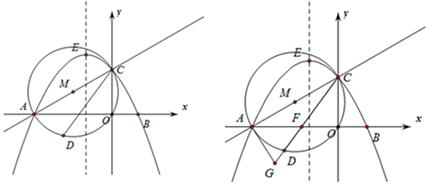
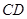 交
交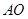 于点
于点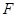 ,延长
,延长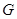 ,使
,使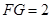 ,试探究当点
,试探究当点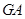 与⊙M相切,并请说明理由.
与⊙M相切,并请说明理由.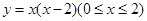 的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m= .
的图象,记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;……如此进行下去,直至得C14. 若P(27,m)在第14段图象C14上,则m= .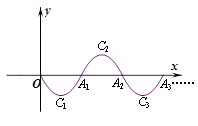
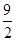 ,则二次函数的解析式是________.
,则二次函数的解析式是________.