题目内容
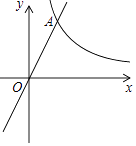
【题目】如图，经过原点的抛物线y=﹣x2+2mx与x轴的另一个交点为A．点P在一次函数y=2x﹣2m的图象上，PH⊥x轴于H，直线AP交y轴于点C，点P的横坐标为1．（点C不与点O重合）
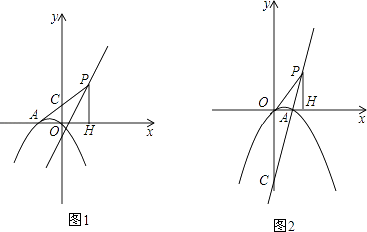
（1）如图1，当m=﹣1时，求点P的坐标．
（2）如图2，当 
时，问m为何值时 
？
（3）是否存在m，使 ？若存在，求出所有满足要求的m的值，并定出相对应的点P坐标；若不存在，请说明理由．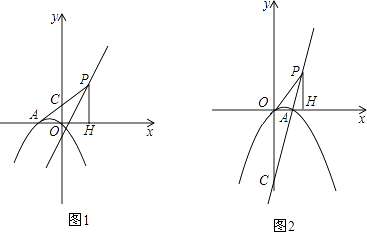
【答案】
（1）
解：如图1，当m=﹣1时，y=2x+2，
令x=1，则y=4，
∴点P的坐标为（1，4）；
（2）
解：如图2，∵PH⊥x轴，
∴PH∥OC，
∴△PAH∽△CAO，
∴ 
= 
，
∵ 
=2，
∴ = =1，
∴OA= 
．
令y=0，则﹣x2+2mx=0，
∴x1=0，x2=2m，
∴点A的坐标（2m，0），
∴2m= ，
∴m= 
；
（3）
解：①当0＜m＜ 时，由（2）得m= ，
∴y=2x﹣ ，
令x=1，则y= 
，
∴点P的坐标为（1， ）；
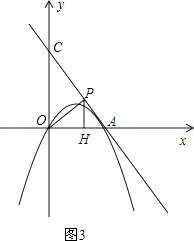
②如图3，当 ≤m＜1时，
∵PH⊥x轴，
∴PH∥OC，
∴△APH∽△ACO，
∴ = ，
∵ =2，
∴ = 
，
∴OH= 
OA，
∵OH=1，
∴OA= ，
∴2m= ，m= 
，
∴y=2x﹣ ，
令x=1，则y= ，
∴点P的坐标为（1， ）；
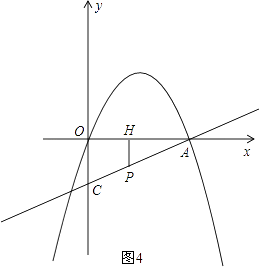
③如图4，当m≥1时，
∵PH⊥x轴，
∴PH∥OC，
∴△APH∽△ACO，
∴ = ，
∵ =2，
∴ = ，
∴OH= OA，
∵OH=1，
∴OA= ，
∴2m= ，m= ，
∵m＞1，∴m= 舍去；
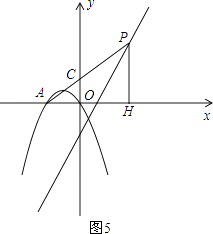
④如图5，当m≤0时，
∵PH⊥x轴，
∴PH∥OC，
∴△APH∽△ACO，
∴ = ，
∵ =2，
∴CP＞AP，
又∵CP＜AP，
∴m的值不存在．
【解析】（1）先将m=﹣1代入y=2x﹣2m，得到y=2x+2，再令x=1，求出y=4，即可求出点P的坐标；（2）先由PH∥OC，得出△PAH∽△CAO，根据相似三角形对应边成比例得到 = ，由 =2，得出OA= ，再解方程﹣x2+2mx=0，求出点A的坐标（2m，0），则2m= ，m= ；（3）分四种情况讨论：①当0＜m＜ 时，由（2）得m= ，将m= 代入y=2x﹣2m，得到y=2x﹣ ，再将x=1代入，求出y的值，得到点P的坐标；
②当 ≤m＜1时，先由PH∥OC，得出△APH∽△ACO，根据相似三角形对应边成比例得到 = ，由 =2，得出OA= ，解方程2m= ，得出m= ，再同①；③当m≥1时，同②，求出m= 舍去；④当m≤0时，先由PH∥OC，得出△APH∽△ACO，根据相似三角形对应边成比例得到 = ，由 =2，得出CP＞AP，而CP＜AP，所以m的值不存在．
【考点精析】解答此题的关键在于理解二次函数的概念的相关知识，掌握一般地，自变量x和因变量y之间存在如下关系：一般式：y=ax2+bx+c(a≠0，a、b、c为常数)，则称y为x的二次函数，以及对二次函数的图象的理解，了解二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点．
