题目内容
【题目】如图，在△ADC中，点B是边DC上的一点，∠DAB=∠C， 
= 
．若△ADC的面积为18cm，求△ABC的面积． 
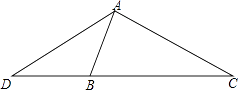
【答案】解：∵∠DAB=∠C，∠D=∠D， ∴△ADC∽△BAD，
∴ 
=（ 
）2=（ 
）2= 
，
∵△ADC的面积为18cm2 ，
∴△BDA的面积为8cm2 ，
∴△ABC的面积=△ADC的面积﹣△BDA的面积=10cm2
【解析】根据相似三角形的判定定理得到△ADC∽△BAD，根据相似三角形的面积比等于相似比的平方即可得到结论．
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识，掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
练习册系列答案
阅读快车系列答案
相关题目
