题目内容
【题目】已知∠AOB,作图.
步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;
步骤2:过点M作PQ的垂线交 ![]() 于点C;
于点C;
步骤3:画射线OC.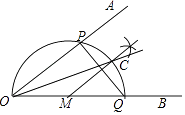
则下列判断:① ![]() =
= ![]() ;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为( )
A.1
B.2
C.3
D.4
【答案】C
【解析】∵OQ为直径,
∴∠OPQ=90°,OA⊥PQ.
∵MC⊥PQ,
∴OA∥MC,结论②正确;
∵OA∥MC,
∴∠POQ=∠CMQ.
∵∠CMQ=2∠COQ,
∴∠COQ= ![]() ∠POQ=∠POC,
∠POQ=∠POC,
∴ ![]() =
= ![]() ,OC平分∠AOB,结论①④正确;
,OC平分∠AOB,结论①④正确;
∵∠AOB的度数未知,∠POQ和∠PQO互余,
∴∠POQ不一定等于∠PQO,
∴OP不一定等于PQ,结论③错误.
综上所述:正确的结论有①②④.
所以答案是:C.
【考点精析】关于本题考查的圆周角定理,需要了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.

练习册系列答案
相关题目