题目内容
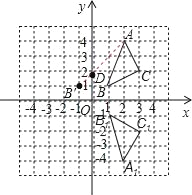
【题目】△ABC在平面直角坐标系中的位置如图.A、B、C三点在格点上.
(1)作出△ABC关于x轴对称的△A1B1C1,并写出点C1的坐标;
(2)在y轴上找点D,使得AD+BD最小,作出点D并写出点D的坐标.

【答案】(1)△A1B1C1如图所示见解析,C1(3,﹣2);(2)点D如图所示见解析,点D的坐标为(0,2).
【解析】
(1)根据网格结构找出点A、B、C关于x轴的对称点A1、B1、C1的位置,然后顺次连接即可,再根据平面直角坐标系写出点C1的坐标;
(2)确定出点B关于y轴的对称点B′,根据轴对称确定最短路线问题连接AB′,与y轴的交点即为所求的点D,然后求出OD的长度,再写出坐标即可.
(1)△A1B1C1如图所示,C1(3,﹣2);
(2)点D如图所示,OD=2,
所以,点D的坐标为(0,2).
故答案为:(1)△A1B1C1如图所示见解析,C1(3,﹣2);(2)点D如图所示见解析,点D的坐标为(0,2).

练习册系列答案
相关题目
【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如图不完整的统计图表.
课外阅读时间频数分布表
课外阅读时间t | 频数 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合计 | 50 | 100% |
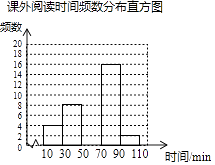
请根据图表中提供的信息回答下列问题:
(1)a= , b=;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?