题目内容
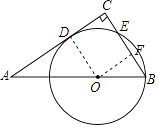
【题目】如图,Rt△ABC中,∠C=90°,BC=3,点O在AB上,OB=2,以OB为半径的⊙O与AC相切于点D,交BC于点E,求弦BE的长.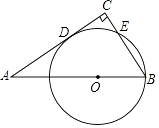
【答案】解:连接OD,作OF⊥BE于点F.
∴BF= ![]() BE,
BE,
∵AC是圆的切线,
∴OD⊥AC,
∴∠ODC=∠C=∠OFC=90°,
∴四边形ODCF是矩形,
∵OD=OB=FC=2,BC=3,
∴BF=BC﹣FC=BC﹣OD=3﹣2=1,
∴BE=2BF=2.
【解析】本题考查了切线的性质、勾股定理及垂径定理的知识,通过辅助线证明四边形OFCD是矩形,得到BF的值,然后利用垂径定理即可求出BE的长.
【考点精析】根据题目的已知条件,利用勾股定理的概念和切线的性质定理的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如图不完整的统计图表.
课外阅读时间频数分布表
课外阅读时间t | 频数 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合计 | 50 | 100% |
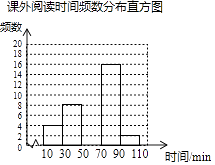
请根据图表中提供的信息回答下列问题:
(1)a= , b=;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?